Resultats de la cerca
Es mostren 67 resultats
Notació, eiπ = –1, línia d’Euler, equació quàrtica, grafs, funció ϕ, funcions beta i gamma, matemàtica aplicada, grans problemes (Euler)
Notació, e iπ = –1, línia d’Euler, equació quàrtica, grafs, funció ϕ , funcions beta i gamma, matemàtica aplicada, grans problemes Euler
funció beta
Matemàtiques
Funció definida per l’equació
que convergeix per a valors de r i s positius.
Anomenada també primera integral d’Euler, és relacionada amb la segona integral d’Euler funció gamma per l’equació
equacions de Lagrange
Física
Equacions diferencials que descriuen el moviment d’un sistema mecànic.
Donat un sistema de coordenades generalitzades, és a dir, un sistema qualsevol de coordenades q 1 , q 2 , , q n que permeti d’especificar les posicions de les partícules del sistema mecànic, les n equacions de Lagrange, una per a cadascuna de les coordenades generalitzades, són on L és el lagrangià i q i la velocitat generalitzada, és a dir, la derivada respecte al temps de la coordenada q i Les equacions de Lagrange, establertes ja per Euler i anomenades també d’Euler-Lagrange , són, en la major part dels problemes interessants, equivalents a les equacions de…
pi
Matemàtiques
Lletra grega, inicial del mot grec περιφέρεια (‘circumferència’)..
És adoptada per a representar la raó constant que existeix entre la longitud de la circumferència i el seu diàmetre longitud de la circumferència, 2πR àrea del cercle, πR 2 àrea de l’esfera, 4πR 2 volum de l’esfera, L’ús d’aquesta llegra grega per a designar la relació entre la longitud de la circumferència i el seu diàmetre es remunta solament al s XVII, i es generalitzà a partir de la publicació de l’obra d’Euler Introductio in analysim infinitorum el mateix Euler i JBernoulli usaren P i c , respectivament, com a símbol representatiu A Egipte hom havia fet…
teorema de Fermat
Matemàtiques
Teorema segons el qual si p és un nombre primer i a un nombre primer amb p, aleshores es satisfà que ap-1—1 és divisible per p, o sigui, ap-1≡(mod p).
La primera demostració d’aquest teorema fou feta per Euler el 1736
Johann Bernoulli
Matemàtiques
Matemàtic suís.
Començà estudiant medicina, però es decantà molt aviat per les matemàtiques Fou deixeble del seu germà Jakob, que l’inicià en l’obra de Leibniz, de la qual fou propagador Estigué a París 1690-95, on redactà un curs de càlcul per al marquès de L’Hôpital hom creu que la coneguda regla de L’Hôpital és deguda a Johann Bernoulli El 1691 determinà les tangents i els radis de curvatura de moltes corbes planes i donà el primer exemple de coordenades polars Fou professor a Groningen 1695-1705 i, des de la mort del seu germà Jakob, a Basilea 1705, on fou mestre d’Euler Proposà i resolgué…
factorial
Matemàtiques
Producte dels nombres naturals consecutius, des de l’1 fins al nombre del qual hom calcula el factorial.
És indicat per n La generalització de la noció de factorial a nombres no naturals és possible mitjançant la funció Γ d’Euler gamma Per a molt gran, hom pot calcular n aproximadament per mitjà de la fórmula de Stirling
univers
Matemàtiques
Conjunt de referència els subconjunts del qual són utilitzats en un raonament concret.
En els diagrames de Venn-Euler hom sol representar l’univers amb un rectangle, dins el qual són dibuixats els diagrames dels conjunts que hom vol representar Així, en l’estudi dels conjunts de nombres reals l’univers és ℝ
diagrama de Venn
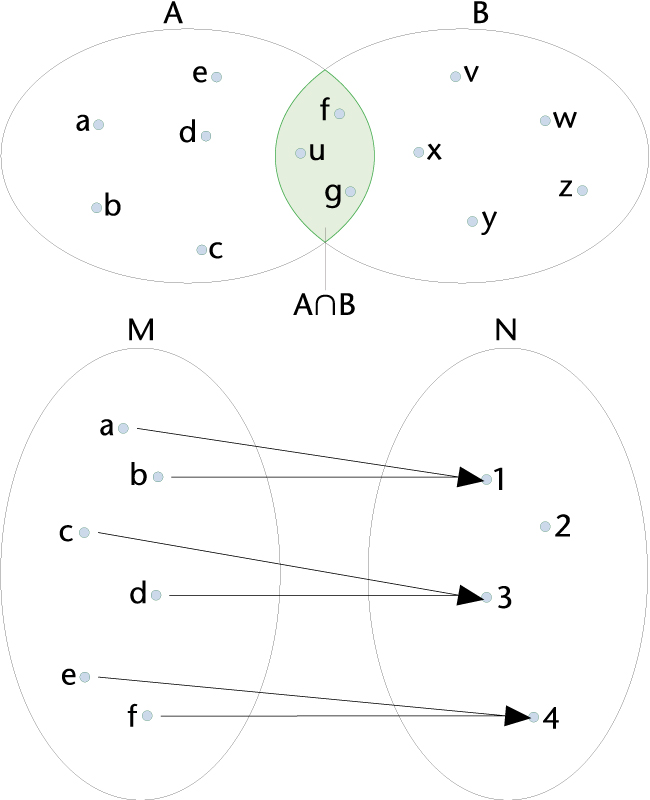
Representació de la intersecció dels conjunts A i B (a dalt) i de l’aplicació del conjunt M en el conjunt N (a baix) per mitjà de diagrames de Venn
© Fototeca.cat
Matemàtiques
Diagrama emprat amb fins didàctics per a representar gràficament conjunts i estudiar les relacions i operacions entre conjunts.
Aquests diagrames foren introduïts pel matemàtic i lògic anglès John Venn 1834-1923 Els conjunts són representats mitjançant cercles o corbes tancades qualssevol Cal no confondre un diagrama de Venn amb la regió del pla limitada pel diagrama És conegut també com a diagrama d’Euler-Venn
principi de Maupertuis
Física
Forma simplificada del principi de Hamilton de la mecànica analítica que permet de trobar la trajectòria d’una partícula sense cap referència al temps, posat que la funció de Hamilton de la partícula no depengui explícitament del temps.
Enunciat primitivament per Maupertuis, de qui pren el nom, fou establert en forma matemàtica per Euler i Lagrange finalment, Jacobi el posà en la forma , on m és la massa de la partícula, E l’energia total, U l’energia potencial, quan la partícula és sotmesa a forces conservadores, i dl un element de longitud de la trajectòria