Resultats de la cerca
Es mostren 46 resultats
llei de Lambert
Electrònica i informàtica
Física
Llei en virtut de la qual la il·luminació d’una superfície és inversament proporcional al quadrat de la distància que la separa del focus lluminós i directament proporcional al cosinus de l’angle que formen els raigs lluminosos amb la normal a la superfície.
És anomenada correntment llei del cosinus illuminació
cercle goniomètric
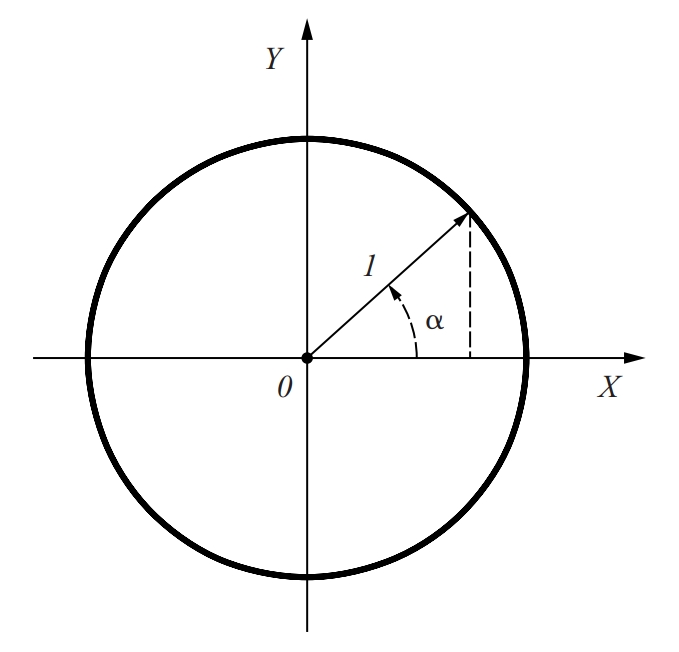
cercle goniomètric
Matemàtiques
Circumferència de radi unitat el centre de la qual és l’origen d’un sistema de coordenades cartesianes (eixos perpendiculars).
És emprat per a definir les raons trigonomètriques d’un angle sinus, cosinus, tangent, etc
reducció a l’horitzó
Geografia
Operació consistent a trobar el valor de la distància horitzontal corresponent a la distància real entre dos punts del terreny.
Per a fer la reducció a l’horitzó cal multiplicar aquesta darrera distància pel cosinus de l’angle del pendent del terreny
fasímetre
Física
Aparell per a mesurar la diferència de fase φ entre dues magnituds elèctriques alternes de la mateixa freqüència, com és el cas de dues tensions o dos corrents d’un sistema polifàsic o del desfasament entre la tensió i el corrent en una mateixa fase.
L’aparell és de tipus electrodinàmic i duu una escala graduada que pot indicar l’angle φ o, més correntment, el seu cosinus cos φ
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament, fàcils de traçar A partir de…
JPEG 2000
Electrònica i informàtica
Norma de compressió d’imatges basada en la transformació d’ondetes.
Presenta una millora de l’estàndard JPEG basada en la transformació discreta del cosinus Normalment els arxius amb aquest format utilitzen l’extensió jp2 Part del JPEG 2000 ha estat publicada com a norma ISO/IEC 15444-12000t
funció periòdica
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
terme
Matemàtiques
Cadascuna de les parts que formen una expressió algèbrica additiva.
Així, en 5 x 2 -3 x+2 hi ha tres termes 5 x 2 , -3 x i +2 En general hom parla de termes algèbrics, trigonomètrics, exponencials, logarítmics , etc, segons que les variables apareguin afectades per les respectives funcions algèbriques polinomis, trigonomètriques sinus, cosinus, tangent, etc
funció tangent
Pla tangent i dues rectes tangents a la superfície z=f(x,y) en el punt P
© Fototeca.cat
Matemàtiques
Funció tg: →-{π/2+kπ, k ∈ℤ} →ℝ, definida per l’assignació x
→tg x
, on tg x
és la tangent de l’angle que fa x
radiants.
És una funció periòdica de període 2 i el seu recorregut és -∞, ∞ És una de les sis funcions trigonomètriques o circulars i està relacionada amb les funcions sinus i cosinus per l’expressió tg x =sin x /cos x És indefinidament derivable i el seu desenvolupament en sèrie entera és quan x 2
funció exponencial complexa
Matemàtiques
Funció f:ℂ→ℂque resulat d’estendre a ℂla funció exponencial.
És anomenada també, simplement, exponencial complexa És definida per l’assignació on z ∈ℂ És periòdica de període 2π i És relacionada amb les funcions trigonomètriques sinus i cosinus per la relació e x + i y = e x cos y + sin y , que permet excriure la forma exponencial d’un nombre complex, z = x + iy = ρ e i ϑ on és el mòdul de z i ϑ = arc tg y/x n'és l’argument