Resultats de la cerca
Es mostren 139 resultats
bosó
Física
Partícula que obeeix l’estadística de Bose-Einstein.
Són bosons les partícules elementals o compostes que tenen spin enter així, ho són el fotó, els pions i els kaons, i gairebé tots els mesons, com també l’àtom d’hidrogen, el deuteró, l’àtom d’heli i, en general, els nuclis atòmics de nombre nucleònic parell
ponsètia

ponsètia
Botànica
Planta arbustiva, de la família de les euforbiàcies, de fins a 4 m d’alt, de fulles lanceolades o ovatoel·líptiques, enteres o dentades, originària de Mèxic i cultivada per les seves flors vermelles o roses.
Les fulles superiors, més estretes i de marge enter, varien de color a l’època de la floració final de tardor i hivern, tornant-se vermelles, rosades, grogues o blanquinoses Als Països Catalans s’ha convertit en una típica planta d’interior que adorna les cases durant les festes nadalenques
descomposició en factors primers a ℤ
Matemàtiques
.
Propietat del conjunt dels nombres enters ℤ, segons la qual tot enter no nul pot expressar-se d’una manera única en la forma b=sp 1 a 1 p n a n , on s=1 o -1, els p i són nombres primers diferents, i els a i són nombres naturals no nuls
àtom de Bohr
Física
Model atòmic proposat per N.H.D. Bohr el 1913 per a descriure l’àtom d’hidrogen.
Recolza sobre les hipòtesis següents l’àtom només pot existir en uns certs estats estacionaris, caracteritzats pel fet que el seu electró només pot ocupar unes òrbites o nivells energètics ben definides, que, tot i ésser governades per la mecànica clàssica, són determinades per la condició que el moment angular orbital de l’electró sigui un múltiple enter de la constant de Planck reduïda L = nh , essent h = h/ 2π l’emissió i absorció d’energia per l’àtom no es realitza de forma contínua , com demanaria l’electrodinàmica clàssica en explicar el moviment circular dissipatiu d’un…
arc
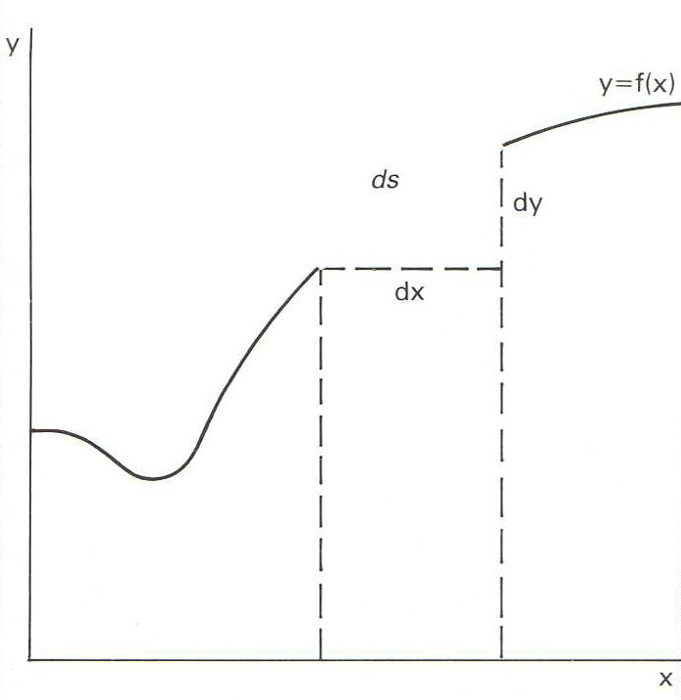
Matemàtiques
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es…
unitat de compte
Economia
Fracció mínima que es fa equivalent a un dels béns que per convenció serveixen per a mesurar el preu de les coses, així com la relació entre elles, i que esdevé una característica essencial en el diner, per la qual hom pot establir una identitat entre unitat de compte i unitat monetària.
Malgrat aquesta identitat, existeixen altres unitats de compte, com ara l’enter equivalent a la centèsima part del valor d’una acció o una obligació, que té la finalitat d’establir el valor d’aquests títols en els mercats borsaris, o les unitats clearing , que, malgrat la referència al valor d’un mitjà de pagament internacional, no són en cap moment diner
sèrie de Balmer
Física
Conjunt de ratlles de l’espectre atòmic de l’hidrogen, que corresponen a les transicions al nivell de nombre quàntic principal n=2; són a la regió visible i a la de l’ultraviolat proper de l’espectre.
Els valors de les diferents longituds d’ona són donats per l’expressió l/λ= R H 1/2 2 -1/ N 2 , essent R H la constant de Rydberg per a l’àtom d’hidrogen R H =109 737 cm - 1 i N un nombre enter més gran que 2 Aquesta equació, deduïda empíricament per JJ Balmer, no rebé una interpretació teòrica correcta fins a l’adveniment del model de l’àtom de Bohr
funció gamma
Matemàtiques
Funció definida per la fórmula, deguda a Euler, Γ( x
) = ∫
t ( x - 1 )
e - t
, on, si hom considera Γ real, x
ha d’ésser real i major que zero, i si hom considera Γ complexa, la part real de x
ha d’ésser major que zer¦.
Segons Gauss, hom pot definir també la funció Γ amb l’expressió on x pot ésser qualsevol nombre real o complex, excepte enter negatiu Les propietats immediates de la funció Γ són Γ x +1 = x Γ x Γ1 = 1 Γ n = n-1 , per a n natural Una aplicació important de la funció Γ és que permet de generalitzar el concepte de factorial a nombres reals no enters i a nombres complexos
potència
Matemàtiques
Donats un nombre a
, anomenat base
, i un nombre natural n
, anomenat exponent
, producte
a n
de n
factors iguals a a
, és a dir,
.
Hom generalitza la noció de potència al cas en què l’exponent és un enter negatiu, mitjançant la fórmula a -n =1/a n , i al cas en què l’exponent és un nombre racional, mitjançant la fórmula La generalització al cas que l’exponent sigui un nombre real qualsevol té lloc mitjançant la funció exponencial , i en el cas que l’exponent sigui un nombre complex, mitjançant la fórmula de De Moivre Les propietats més importants de les potències són
vòrtex quantificat
Física
En un superfluid, vòrtex que apareix en fer-lo girar amb una velocitat per sobre de certa velocitat crítica.
A causa del caràcter univaluat de la funció d’ona que descriu el superfluid d’acord amb la mecànica quàntica, un vòrtex tan sols pot existir en un superfluid si, en girar al seu voltant, el fluid adquireix un moment angular que és un múltiple enter de ħ, la constant de Planck dividida per 2π S'han observat vòrtexs quantificats en heli superfluid, en metalls superconductors i en gasos atòmics ultrafreds, la qual cosa ha servit per a demostrar-ne inequívocament el caràcter superfluid