Resultats de la cerca
Es mostren 85 resultats
quadrangle
Matemàtiques
Figura plana que té quatre angles i quatre costats, quadrilàter.
quadrat
Matemàtiques
Quadrilàter amb els quatre costats iguals i els quatre angles rectes.
L’àrea d’un quadrat de costat a és a 2
paral·lelogram
Matemàtiques
Quadrilàter que té els costats oposats paral·lels i, per tant, iguals.
Les diagonals d’un parallelogram es tallen en llur punt mitjà, anomenat centre del parallelogram Si un parallelogram té els quatre costats iguals, és anomenat rombe Si els quatre costats són perpendiculars, és anomenat rectangle Els parallelograms que són rombes i rectangles alhora són anomenats quadrats , i els que no són ni rombes ni rectangles, romboides L’àrea d’un parallelogram resulta de multiplicar la longitud d’un costat, que hom anomena base , per la distància que el separa del seu parallel, anomenada altura
vòmer
Anatomia animal
Os quadrilàter, laminar, que constitueix l’envà de les fosses nasals.
polígon
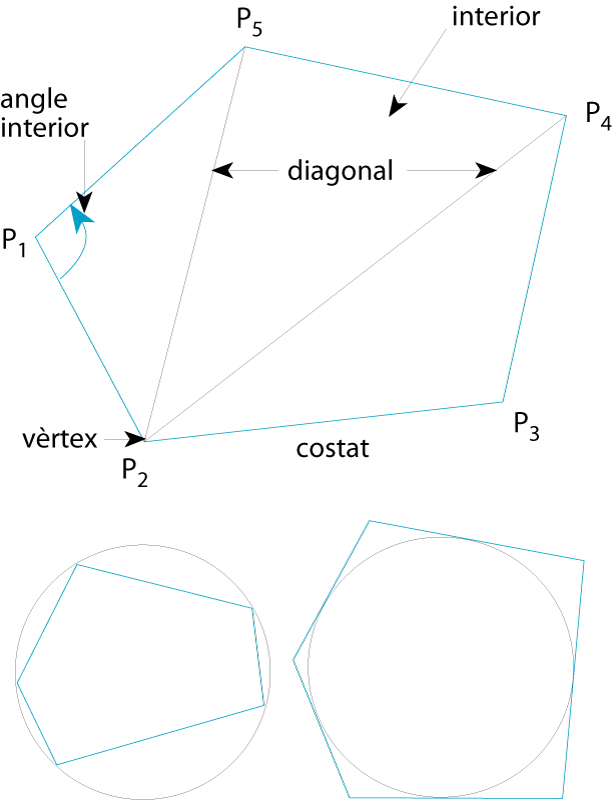
Elements d’un polígon (dalt); polígon inscrit en un cercle (baix esquerre); polígon circumscrit a un cercle (baix dreta)
© Fototeca.cat
Matemàtiques
Figura plana i tancada formada per segments rectes.
P 1 P 2 , P 2 P 3 , P n - 1 P n , i P n P 1 , són anomenats costats del polígon, essent els punts P 1 , P 2 , , P n , amb n ≥3, els anomenats vèrtexs del polígon Una diagonal del polígon és el segment recte que uneix dos vèrtexs no correlatius La porció de pla que és envoltada pels costats constitueix l' interior del polígon Els angles determinats per cada parell de costats adjacents, i que són a l’interior, són dits angles interiors del polígon Un polígon és convex si cada angle interior és menor o igual a 180° Un polígon és còncau si no és convex, és a dir, si almenys existeix un angle…
trapezoide
Matemàtiques
Quadrilàter que no té cap dels seus costats paral·lel a un altre.
les Cluses
Municipi
Municipi del Vallespir, al vessant septentrional de la serra de l’Albera, a la vall mitjana de la ribera de Roma, via de comunicació entre el Rosselló i l’Empordà, a través dels colls de Panissars i del Portús.
El terme és en gran part boscat alzina surera Fins vers el 1850 el municipi comprenia el poble del Portús i el castell de Bellaguarda amb la segregació, la població passà de 744 h el 1846 a 129 el 1851 El centre del municipi és la Clusa d’Amunt a poca distància hi ha els veïnats de la Clusa del Mig i de la Clusa d’Avall, sorgits amb el desplaçament de l’antic camí A l’indret del poble, a banda i banda del riu, hi ha les ruïnes de les dues fortificacions de la Clusa , d’origen romà, que controlaven, des d’altures simètriques, el pas de la via romana que unia la Tarraconense i la Gàllia…
art singalès
Art
Art desenvolupat a Sri Lanka.
La història de l’art de Sri Lanka és dividida d’acord amb les successives capitals reials en tres grans períodes el període d’Anurād-hapūraya segle IV aC — VIII dC es caracteritza en el camp de l’arquitectura per les dagoba , adaptació dels stupa indis Les principals són les de Ruvanveli segle II aC, Thūpārāma segle III aC i Jetavana segle IV dC Les dagoba eren envoltades de monestirs, l’exemple cabdal dels quals és el Lohapāsāda o Palau de Bronze L’escultura és representada per un conjunt de Budes excessivament restaurats i els relleus que ornen les llindes i els esglaons En la pintura cal…
trapezi
Matemàtiques
Quadrilàter que té dos costats oposats paral·lels i els altres dos no paral·lels.
Els dos costats parallels b 1 i b 2 són les bases , i llur distància h és l' altura del trapezi L’àrea és h b 1 + b 2 /2, és a dir, el producte de l’altura per la semisuma de les bases Si els costats no parallels són iguals, és anomenat trapezi isòsceles
as
Numismàtica i sigil·lografia
Unitat base del sistema monetari romà, per a les sèries de coure o de bronze; comprenia dotze unces, com la lliura.
El seu origen no és clar Les teories tradicionals n'assenyalen l’aparició vers l’any 450 aC, mentre que els investigadors de l’escola anglesa proposen la data, molt més tardana, del 269 aC Bé que inicialment tenia l’equivalència d’una lliura de coure, sofrí successivament reduccions molt contínues que el portaren al pes d’una quarta part d’unça En un principi, aparegué com un lingot de forma no definida aes rude o aes infectum Més tard es transformà en un quadrilàter amb una representació figurada i fins i tot una llegenda aes signatum Adaptat el seu pes a la lliura itàlica de 341 g, i més…