Resultats de la cerca
Es mostren 6227 resultats
integral
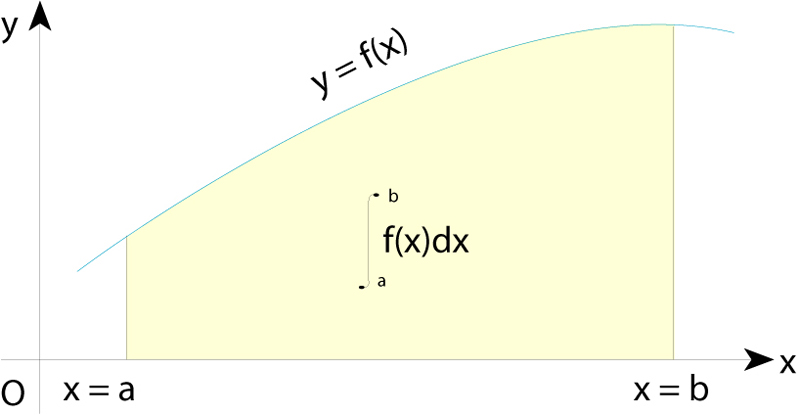
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i…
fotoperíode
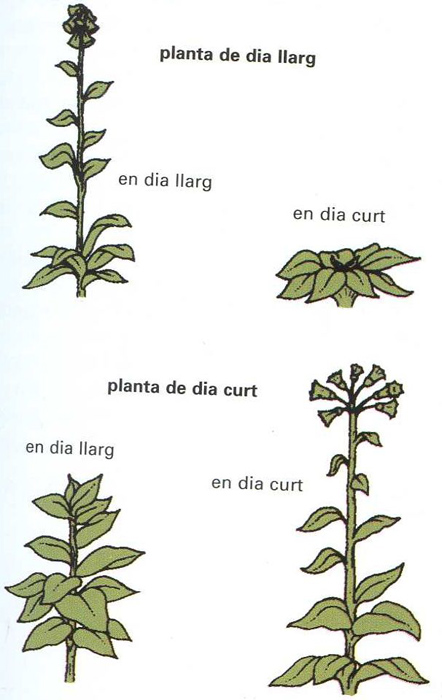
Floració en funció del fotoperíode
© fototeca.cat
Biologia
Botànica
Durada relativa dels períodes de claror i de foscor diaris a què són sotmesos els organismes.
Alternances de períodes de claror i de foscor i llur efecte sobre les plantes de dia curt i de dia llarg En les plantes, el pigment responsable de la resposta al fotoperíode és el fitocrom El fotoperíode influeix sobre molts processos fisiològics de les plantes així s’esdevé en la floració les plantes anomenades de dia llarg necessiten un mínim d’hores de claror perquè hi hagi una elevada proporció de fitocrom actiu, que és el que permet la síntesi de la gibberellina les plantes de dia curt , per contra, no poden sobrepassar un màxim d’hores de claror, puix que per a florir necessiten un baix…
derivable
Matemàtiques
Dit d’una funció que admet derivada.
Més exactament, hom parla de funció derivable a l’esquerra o derivable a la dreta en un punt si la funció té derivada a l’esquerra o a la dreta en aquest punt, respectivament Hom diu que una funció és derivable en un punt si hi és derivable a l’esquerra i a la dreta Hom parla també de funcions derivables en un interval obert o tancat f és derivable en l’interval obert a,b si és derivable en tot punt d’ell, i f és derivable en un interval tancat a,b si és derivable en a,b i ho és a la dreta de a i a l’esquerra de b
aminofenol
Química
Substància orgànica que té almenys una funció amina i una funció fenol.
Els aminofenols en els quals la funció amina és portada per un carboni aromàtic solen obtenir-se per reducció dels nitrofenols o nitrosofenols corresponents i són composts reductors, fàcilment alterables Molts d’ells i els àcids sulfònics que en deriven són intermediaris importants en la síntesi de colorants
equació funcional
Matemàtiques
Relació imposada a una funció.
Una tal relació defineix una funció o família de funcions que satisfan aquella relació
àcid cetònic
Química
Compost orgànic que té almenys una funció àcid carboxílic i una funció cetona.
L’àcid pirúvic, CH 3 COCOOH, és el més simple dels àcids cetònics En virtut de l’efecte inductiu, els àcids cetònics són més forts que els àcids corresponents que no tenen funció cetona
ciutat universitària
Urbanisme
Tipus de ciutat de funció essencialment universitària.
El cas més clar són les ciutats en què aquesta funció predomina sobre tota altra Uppsala, Coïmbra, Göttingen, Cambridge, Aarhus, Lovaina, Princeton, Akademgorodok Els edificis universitaris representen els conjunts més grandiosos, i els serveis ciutadans són en funció dels estudiants que hi resideixen El terme ha estat aplicat també actualment al conjunt d’edificis universitaris d’una ciutat i que formen una petita ciutat especialitzada dins l’àrea urbana Blindern, a Oslo Orsay, a París Fann, a Dakar Berkeley, a San Francisco
integral indefinida

Integrals indefinides de les funcions usuals
©
Matemàtiques
Donada una funció f:(a,b] ⊂ℝ→ℝ, funció F definida en [a,b] per la integral (definida) F(x)= ∫fxsup;a&(t)dt.
Aquesta funció és una funció primitiva de la funció f , per tal com la seva derivada és igual a f , F' x = f x , i, de fet, genera la resta de funcions primitives de f , G x = F x + C , essent C una constant
gradient
Física
Matemàtiques
Donada una funció f
derivable i definida en una regió de l’espai ℝ 3
, funció vectorial (grad f
o ∇ f
) definida per la fórmula
.
En cada punt, és un vector perpendicular a la superfície f = constant, que passa pel punt en què és calculat, i, per tant, té la direcció en la qual varia més ràpidament Per extensió, hom anomena gradient d’una funció en una direcció o derivada direccional la projecció del vector gradient en aquella direcció Així, fixada una direcció, el gradient d’una funció en aquella direcció dóna el ritme de variació de la funció en avançar en la direcció considerada En meteorologia i en física de fluids són molt utilitzats els gradients tèrmics i baromètrics per a…
andropausa
Biologia
Cessació de la funció sexual en l’home.
A diferència de la menopausa, que és la cessació de la funció sexual en la dona, s’esdevé entre límits d’edat molt variables Pot anar acompanyada de trastorns psíquics com ara ansietat, hipocondria, irritabilitat, manca d’atenció i de memòria i tristesa
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- …
- Pàgina següent
- Última pàgina