Resultats de la cerca
Es mostren 578 resultats
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes (Gauss)
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes Gauss
Miguel Colmeiro y Penido publica el Catálogo metódico de las plantas observadas en Cataluña con sus nombres botánicos y en catalán
Miguel Colmeiro y Penido publica el Catálogo metódico de las plantas observadas en Cataluña con sus nombres botánicos y en catalán
teorema de Bernoulli
Matemàtiques
Donat un nombre ε arbitràriament petit, la probabilitat que la diferència entre la freqüència relaiva f de l’esdeveniment favorable en una sèrie de proves i la probabilitat p d’aquest esdeveniment sigui, en valor absolut, superior a ε tendeix a zero en augmentar indefinidament el nombre de proves.
O sigui Aquest teorema fa aparèixer el lligam que hi ha entre freqüència relativa i probabilitat, la qual és el valor mitjà de la freqüència per a un nombre molt gran de proves Com que hi intervé un nombre de proves tant gros, aquest teorema és conegut també amb el nom de llei dels grans nombres
Còniques, cicloide, probabilitat, triangle de Pascal, màquines de computar (Blaise Pascal); àlgebra, nombres imaginaris, longitud d’arc, exponents, símbol infinit, integració (John Wallis); duplicació i quadratures (Grégoire de SaintVincent)...
Còniques, cicloide, probabilitat, triangle de Pascal, màquines de computar Blaise Pascal àlgebra, nombres imaginaris, longitud d’arc, exponents, símbol infinit, integració John Wallis duplicació i quadratures Grégoire de SaintVincent trigonometria, astronomia, projeccions, sèries de logaritmes Mercator
nombre complex
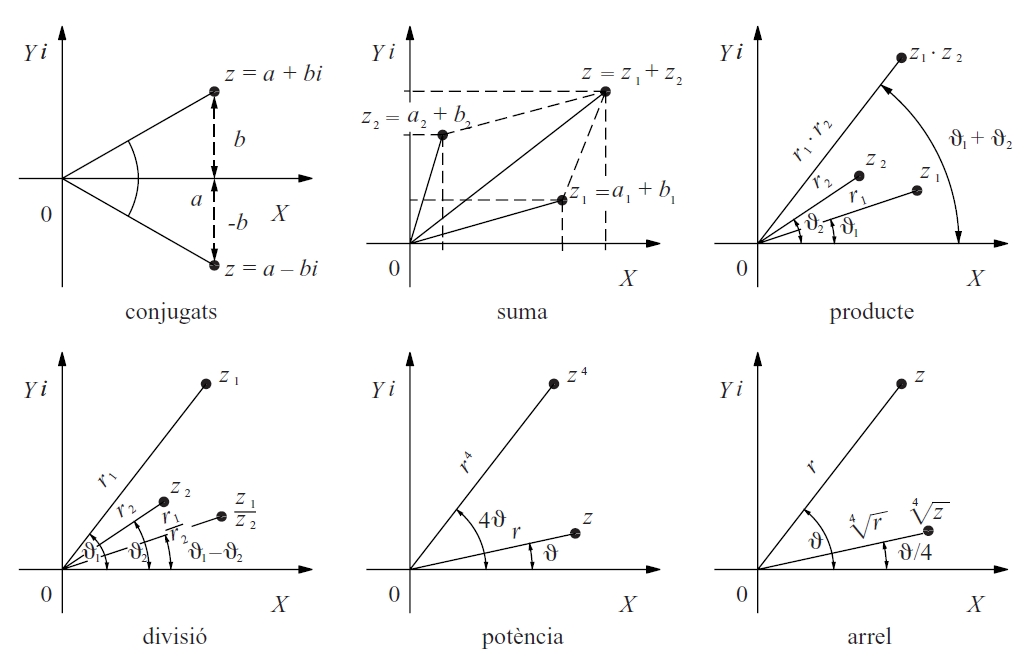
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir…
aritmètica
Matemàtiques
Estudi dels nombres naturals i de les operacions d’addició, subtracció, multiplicació, divisió entera, potenciació i extracció d’arrels enteres entre aquests nombres.
L’aritmètica ha nascut a totes les civilitzacions ensems amb el llenguatge per anomenar conjunts de persones o d’objectes i després per facilitar els intercanvis comercials Els egipcis s’havien ocupat d’alguns problemes aritmètics, i les obres que n'han estat conservades la més antiga de les quals és el papir Rhind ~s XVII aC contenen la resolució d’algunes qüestions numèriques sense dir en quines propietats recolza la resolució, ni menys encara justificar-les El nivell de llurs coneixements era, aproximadament, el de l’actual ensenyament primari, però eren enunciats amb un llenguatge més…
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres…