Resultats de la cerca
Es mostren 243 resultats
teorema de Larmor
Electrònica i informàtica
Física
Teorema segons el qual, en col·locar en el si d’un camp magnètic feble i uniforme un sistema de partícules carregades (com ara els electrons d’un àtom), l’eix de l’òrbita de cada partícula experimenta un lent moviment de precessió al voltant de la direcció del camp.
Aquest fenomen permet d’obtenir informació sobre l’estructura atòmica o molecular
teorema de Cantor
Matemàtiques
Teorema de la teoria de conjunts, segons el qual si C és un conjunt i℘© és el conjunt de tots els subconjunts de C, aleshores se satisfà que card[℘C)] > Card (C) i que card[℘(C)] = 2 card (C) on card és símbol de cardinal d’un conjunt.
teorema de Liouville
Física
Teorema segons el qual els punts de l’espai fàsic (cadascun dels quals representa un possible estat del sistema material donat) es mouen, en el decurs del temps, com un fluid incompressible, és a dir, que el volum de l’espai fàsic ocupat per un conjunt d’aquests punts roman constant.
teorema de Ptolemeu
Matemàtiques
Teorema segons el qual la condició necessària i suficient perquè un quadrilàter convex sigui inscriptible en un cercle és que el producte de les diagonals sigui igual a la suma dels productes dels costats oposats, és a dir, si A, B, C i D són els vèrtexs del quadrilàter, la condició es AC · BD = AB · CD + AD · BC.
teorema de Bézout
Matemàtiques
Teorema segons el qual el nombre de solucions d’un sistema de n equacions polinòmiques (sense factors en comú per a totes) en n variables, de graus respectius m1,...,mn, és el producte d’aquests: N = m1 · m2...mn (cal tenir en compte les multiplicitats de les solucions i l’eventualitat de solucions infinites).
Com a cas particular, fent n =2, resulta que dues corbes algèbriques planes, d’ordres respectius m 1 i m 2 , tenen m 1 m 2 punts d’intersecció iguals o no
teorema d’Apol·loni
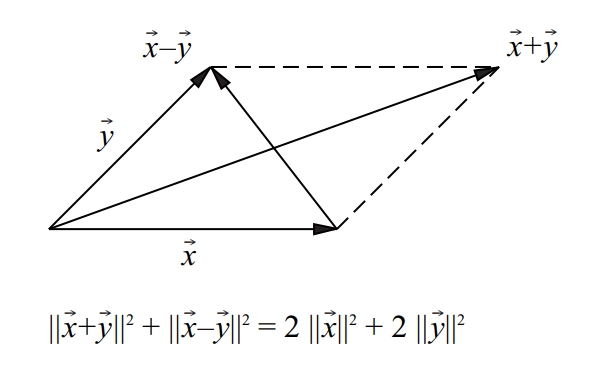
Formulació vectorial del teorema d’Apol·loni
Matemàtiques
Teorema de geomètria mètrica segons el qual en tot triangle la suma dels quadrats de dos costats és igual al doble de la suma del quadrat de la meitat del tercer costat més el quadrat de la mitjana corresponent a aquest darrer costat.
En la seva formulació actual, amb vectors i normes, aquest teorema s’anomena també llei del parallelogram i estableix que la suma dels quadrats de les dues diagonals del parallelogram és igual a la suma dels quadrats dels quatre costats
teorema de Bolzano-Cauchy
Matemàtiques
Teorema referit a l’estudi de la convergència de funcions.
Estableix que la condició necessària i suficient perquè la funció y x sigui convergent en x →η és que, per a cada nombre ε > 0, es compleixi per a tot parell de valors x’, x' d’un cert entorn reduït de η l’acotació | y x' - y x' | < ε Aquest teorema referit a la convergència de funcions és aplicat a la teoria de sèries quan la variable és natural i d’integrals
teorema dels increments finits
Matemàtiques
Teorema segons els qual si f(x) és una funció contínua en [a,b] i derivable en (a,b), aleshores existeix almenys un punt c ∈(a,b) tal que .
També és anomenat teorema del valor mitjà
teorema central del límit
Matemàtiques
Teorema segons el qual, per a una distribució de probabilitat arbitrària de mitjana μ i variància σ2, i essent x̄ la mitjana de n observacions independents d’aquesta distribució, la variable
té una distribució
.
Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/ n de la d’aquesta A la pràctica, per a n ≥ 10 l’aproximació és ja suficient Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries Això explica per què a la pràctica hi ha moltes…
teorema dels quatre colors
Cartografia
Teorema proposat per F. Guthrie a Augustus De Morgan el 1852, que afirmava que eren suficients quatre colors diferents per a colorar qualsevol mapa (és a dir, qualsevol divisió d’un pla o d’una esfera en regions), de manera que les regions amb frontera comuna tinguessin coloracions diferents.
Aquest teorema restà sense demostrar tot i que en general n’era acceptada la validesa fins l’any 1976 quan els matemàtics Kenneth Appel i Wolfgang Haken demostraren a partir de càlculs realitzats per ordinador que, efectivament, n'hi ha prou amb quatre colors per a colorar un mapa sense que hi hagi dues divisions adjacents del mateix color
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- …
- Pàgina següent
- Última pàgina