Resultats de la cerca
Es mostren 218 resultats
sistema de coordenades
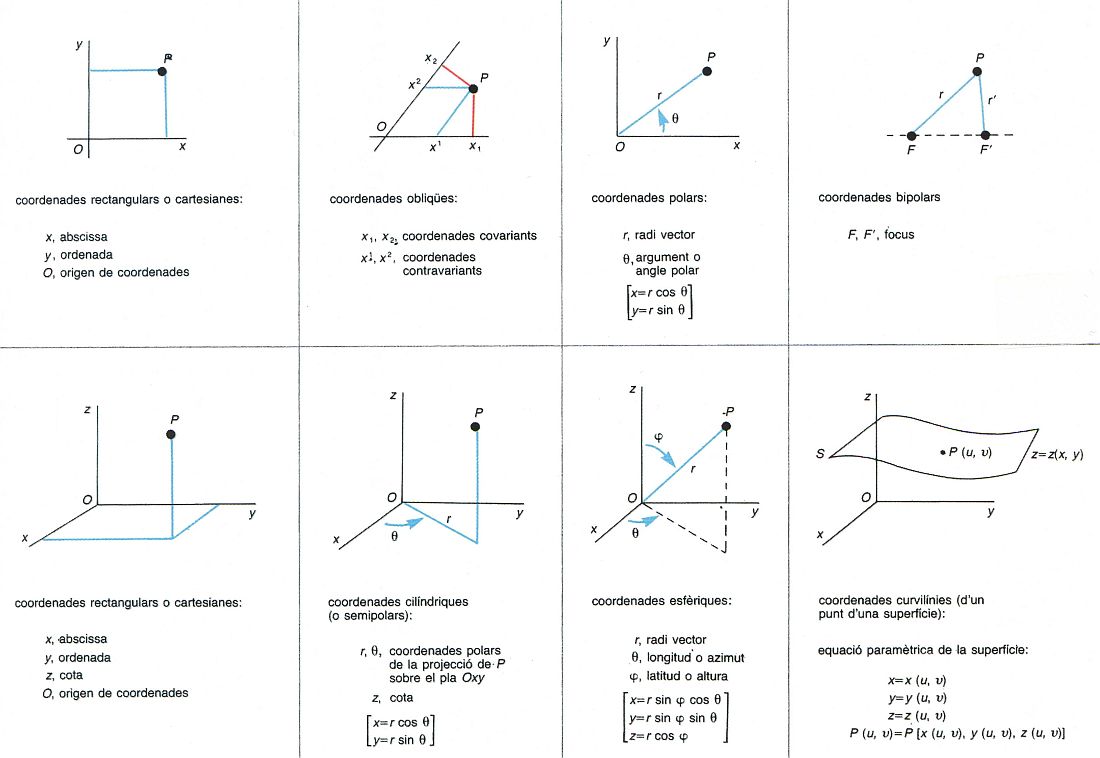
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
equació de Schrödinger
Física
Equació diferencial fonamental de la mecànica quàntica, que permet de calcular la funció d’ona ψ (x,t) d’una partícula sotmesa a una dinàmica especificada per un potencial V (x,t).
Formulada el 1926 per Erwin Schrödinger, hom l’escriu on h és la constant de Planck normalitzada és a dir, dividida per 2π, m la massa de la partícula, V el potencial a què es troba sotmesa, x el vector de posició, t el temps i i la unitat imaginària
dependència lineal
Matemàtiques
En un espai vectorial E sobre un cos C, relació entre un conjunt de vectors, v 1,..., v n, tals que existeixen nombres de C, a1,...,an, algun d’ells no nul, amb els quals se satisfà que a1 v 1+...+an v n=0
.
Els vectors v 1 ,, v n són aleshores linialment dependents A partir de l’anterior expressió hom pot expressar cada vector com a combinació lineal dels altres Si no existeix cap conjunt d’escalars a i que satisfacin l’anterior condició, hom diu que els vectors v i són linealment independents
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…
John Henry Poynting
Física
Físic anglès.
Estudià a Cambridge Féu importants recerques sobre la radiació i el transport de l’energia en els camps electromagnètics vector de Poynting Mesurà la densitat de la Terra i la constant de la gravitació Publicà diverses obres, com Text-Book of Physics 1899-1914, The Pressure of Light 1910 i The Earth 1913
superfície desenvolupable
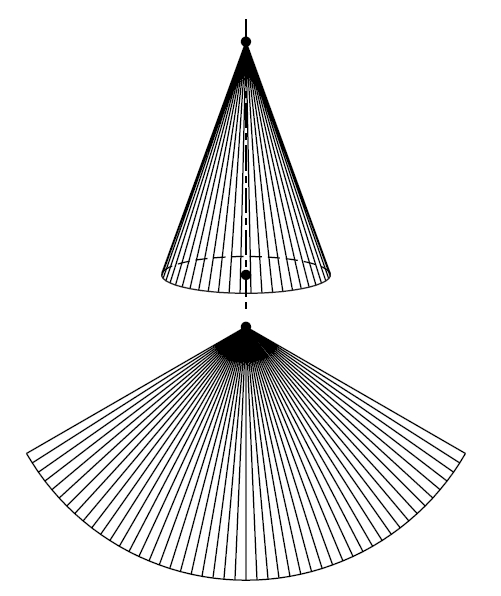
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
magnitud física
Física
Qualsevol propietat dels cossos capaç d’ésser mesurada: longitud, àrea, volum, velocitat, temperatura, força, resistència elèctrica, etc.
Hom classifica les magnituds en escalars , vectorials o tensorials segons que llurs valors puguin ésser expressats utilitzant només un nombre o bé utilitzant un vector o un tensor Una magnitud és anomenada fonamental quan hom la defineix sense recórrer a d’altres magnituds, mentre que en el cas contrari és anomenada derivada Aquestes magnituds derivades poden ésser dimensionals o adimensionals anàlisi dimensional
ortogonalització de Gram-Schmidt
Matemàtiques
En un espai vectorial de dimensió finita n i dotat d’un producte intern <, >, procés que permet d’obtenir una base ortogonal {w1,...,wn} a partir d’una base qualsevol {v1,...,vn} de l’espai.
El procés consisteix a fer w 1 = v 1 , i, per a k ≥2, el k -èsim vector és donat per l’expressió La base formada pels vectors w i /∥ w i ∥, i =1,, n , és una base ortonormal El procés que determina aquesta base, procés que és la combinació de l’ortogonalització de Gram-Schmidt i d’una ortonormalització, és anomenat ortonormalització de Gram-Schmidt
parell de forces
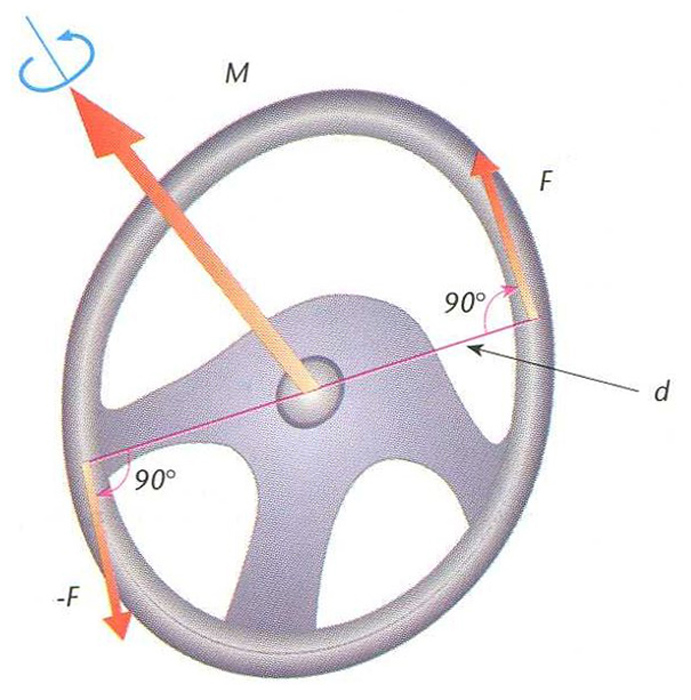
Parell de forces . Representació del moment del parell M en un volant (d distància entre les rectes d’aplicació de les forces F i -F)
© Fototeca.cat
Física
Sistema constituït per dues forces d’igual mòdul, paral·leles i de sentit contrari (i, per tant, de resultant nul·la) i tals que les rectes d’aplicació no són coincidents.
Un parell de forces és caracteritzat per l’anomenat moment del parell , que és un vector el mòdul del qual és el producte del mòdul de les forces del parell per la distància que separa les rectes d’aplicació, és perpendicular al pla de parell i el seu sentit és el sentit en què avança un cargol que giri en el sentit que indiquen les forces del parell
seminorma
Matemàtiques
Aplicació d’un espai vectorial E en el conjunt de nombres reals positius.
A tot vector x de E assigna un valor ∥ x ∥ de manera que ∥ a x ∥ = | a | ∥ x ∥, i que, per a tot x, y de E , ∥ x + y ∥ ≤∥ x ∥ + ∥ y ∥ Si una seminorma compleix, a més, que ∥ x ∥=0 implica x = 0, aleshores es tracta d’una norma En ℝ 2 el pla, ∥ x , y ∥ = | x + y | és una seminorma que no és norma Tota norma és seminorma, però no inversament
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- …
- Pàgina següent
- Última pàgina