Resultats de la cerca
Es mostren 163 resultats
valor propi
Matemàtiques
Donat un operador A en un espai vectorial, escalar α que satisfà A ν = α ν per a algun vector ν no nul, que és aleshores un vector propi de l’operador A.
El conjunt dels valors propis d’un operador és l' espectre de l’operador
fusta
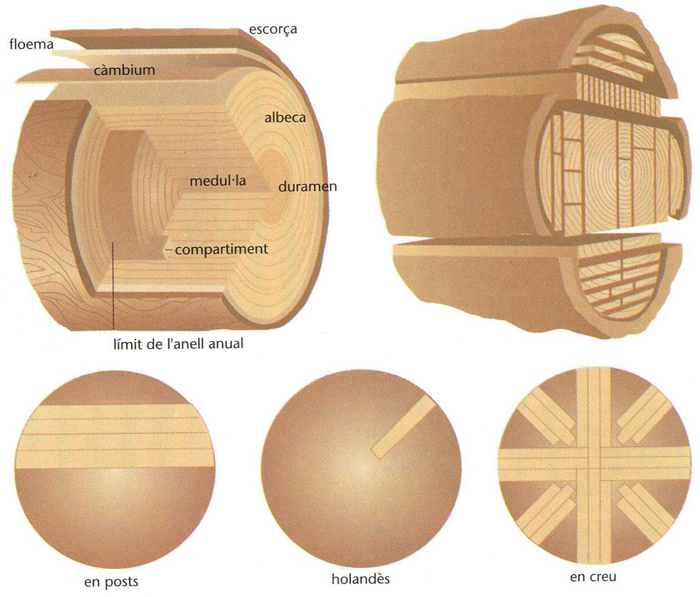
Fusta .Parts d’un tronc i sistemes de serrar-lo per a l’obtenció de taulons
© Fototeca.cat
Tecnologia
Matèria llenyosa de l’arbre.
La substància lígnia es caracteritza pels feixos de fibres separats entre ells per ramades medullars en sentit radial aquestes, de vegades molt aparents, reben el nom de malles i formen teixits en capes successives de període anual La part més ferma i compacta és la més propera al cor, i la més feble i blanquinosa és l’albeca, immediata a l’escorça La matèria que el tronc aporta és apta per a la construcció de bastiments i de mobiliari Hom anomena fusta tova aquella que, com la d’avet o la de balsa, tenen poc pes específic, fusta dura la que té un pes específic elevat, com la del pi resinós,…
matriu ortogonal
Matemàtiques
Matriu quadrada invertible la transposada de la qual és igual a la seva inversa: A t =A-1; una matriu ortogonal satisfà AA t =AtA=I, on I és la matriu unitat.
funció convexa
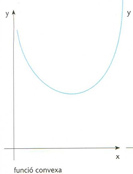
Funció convexa
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1-α)y)≤αf(x)+1-α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sobre de l’arc que uneix f x amb f y
funció contínua a la dreta en un punt
Matemàtiques
Funció f:D⊂ℝ→ℝtal que per al punt a en qüestió satisfà que donat un ε>0 existeix un δ(a,ε)>0 tal que si |x-a|<δ, amb x>a, aleshores |f(x)-f(a)|<ε.
teorema de Fermat
Matemàtiques
Teorema segons el qual si p és un nombre primer i a un nombre primer amb p, aleshores es satisfà que ap-1—1 és divisible per p, o sigui, ap-1≡(mod p).
La primera demostració d’aquest teorema fou feta per Euler el 1736
funció exponencial
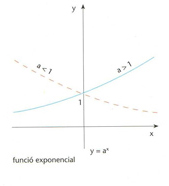
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la funció…
aplicació n-lineal alternada
Matemàtiques
Sobre un espai vectorial, aplicació n-lineal que satisfà que f
( x s ( 1 )
, ..., x s ( n )
) = ε(σ) f
(
x 1
, ..., x n
), on σ és una permutació del conjunt (1, 2, ..., n
) i ε(σ) és la signatura de σ.
la Llagosta

La Llagosta
© Fototeca.cat
Municipi
Municipi del Vallès Oriental, situat en un pla, a la dreta del Besòs.
Situació i presentació Limita amb els municipis de Sant Fost de Campsentelles E, Mollet del Vallès N, Montcada i Reixac S-SW i Santa Perpètua de Mogoda NW, els dos últims pertanyents a la comarca del Vallès Occidental El municipi de la Llagosta se segregà el 1945 del terme de Sant Fost de Campsentelles El poble de la Llagosta està situat entre la riera de Caldes i la riera Seca el terme, a l’altra banda d’aquesta, forma com una llenca de terreny que s’endinsa vers ponent, envoltada pels municipis de Santa Perpètua i Montcada i Reixac El límit de migdia coincideix, en bona part, amb la vora…
Sant Julià de Cerdanyola (Guardiola de Berguedà)
Art romànic
L’actual església de Sant Julià de Cerdanyola és obra del segle XVIII, un edifici de transició entre el barroc i el neoclàssic que anullà totalment l’obra romànica anterior El lloc de Cerdanyola és esmentat ja el segle X com una possessió del monestir de Sant Llorenç prop Bagà L’any 983 en la consagració de l’església monacal és referenciada la villa de Cerdanyola Et in villa Cerdaniola masos X cum terras et vineas et suis terminis L’església de Sant Julià no és citada, però, fins el segle XI, quan és mencionada en l’acta de consagració de Santa Maria de la Seu d’Urgell Cerdaniola , amb la…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- …
- Pàgina següent
- Última pàgina