Resultats de la cerca
Es mostren 154 resultats
Còniques, quadratures, equacions (Menecme, Dinostrat)
Còniques, quadratures, equacions Menecme, Dinostrat
Còniques, llocs geomètrics, tangències, propietats mètriques, cercle i esfera, π val 211875/67441, espirals, sèries, mecànica, hidrostàtica (Arquimedes, Apol·loni).
Còniques, llocs geomètrics, tangències, propietats mètriques, cercle i esfera, π val 211875/67441, espirals, sèries, mecànica, hidrostàtica Arquimedes, Apolloni
Còniques, cicloide, probabilitat, triangle de Pascal, màquines de computar (Blaise Pascal); àlgebra, nombres imaginaris, longitud d’arc, exponents, símbol infinit, integració (John Wallis); duplicació i quadratures (Grégoire de SaintVincent)...
Còniques, cicloide, probabilitat, triangle de Pascal, màquines de computar Blaise Pascal àlgebra, nombres imaginaris, longitud d’arc, exponents, símbol infinit, integració John Wallis duplicació i quadratures Grégoire de SaintVincent trigonometria, astronomia, projeccions, sèries de logaritmes Mercator
cònica
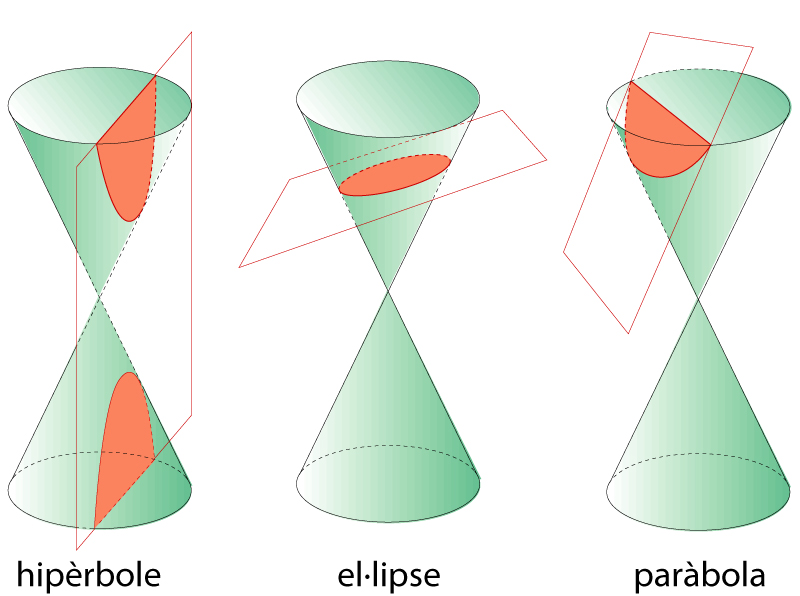
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la…
projecció

Diversos sistemes de projecció. projeccions còniques: cònica simple, cònica secant, Lambert; projeccions cilíndriques: Mercator, transversal de Mercator, UTM; projeccions zenitals (o planes): ortogràfica, estereogràfica, gnomòtica; projeccions preudo-cilíndriques: homologràfica (o de Mollweide), sinusoidal (o de Mercator-Sanson-Flamsteed), homolosiana (o de Goode)
© Fototeca.cat
Cartografia
Acció i resultat de representar una regió de la superfície terrestre sobre un pla.
Una projecció consisteix, en essència, a especificar un mètode per a fer correspondre els punts del globus terraqüi sia representat en la forma d’una esfera, d’un ellipsoide o d’un geoide amb els punts del pla escollit, que és necessàriament el resultat del desenvolupament d’una superfície desenvolupable La correspondència entre els punts del globus i els punts de la superfície desenvolupable pot fer-se de diverses maneres hom empra actualment més de dues-centes projeccions En aquest pas, es produeixen inevitablement algunes de les següents alteracions deformació de l’escala l’escala no és la…
Aristeu de Crotona
Matemàtiques
Matemàtic grec.
Escriví cinc llibres sobre Els llocs sòlids on formulà teoremes sobre els cinc sòlids regulars i sobre les corbes còniques Influí sobre Euclides, bé que el tractat d’Aristeu és més important i original Les seves obres només són conegudes per referències de Pappus i Euclides Això fa que tota l’originalitat de l’estudi de les còniques recaigui sobre Apolloni de Perge
con
Matemàtiques
Superfície reglada generada per totes les rectes (generatrius) que passen per un punt dit vèrtex i per una corba (exterior al punt donat) dita directriu.
La superfície consta de dos fulls units pel vèrtex Es parla de con de revolució si la superfície cònica és engendrada per una recta que passa pel vèrtex i gira al voltant d’una altra recta que també hi passa, la qual és anomenada eix del con Les corbes obtingudes en tallar un con de revolució amb un pla que no passa pel vèrtex reben el nom de seccions còniques o, simplement, còniques Si el pla secant és parallel a una generatriu del con, la cònica rep el nom de paràbola en la resta de casos, el pla secant determina una ellipse o una hipèrbola, segons si el pla…
orbitolina
Paleontologia
Gènere de protozous rizòpodes de l’ordre dels foraminífers, de la família dels orbitolínids, que tenen la closca cargolada en hèlix cònica d’1 a 3 cm de diàmetre.
N'hi ha formes còniques i formes lenticulars, i eren propis del Cretaci
focus
Matemàtiques
Punt la distància del qual a qualsevol dels punts d’una corba pot ésser expressada com una funció racional de les coordenades dels punts.
Aquesta definició mètrica de focus, que és una generalització dels focus de les còniques cònica, no permet, però, d’ésser estesa a una corba algèbrica qualsevol, i per aconseguir-ho cal passar a la definició projectiva de focus
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina