Resultats de la cerca
Es mostren 46 resultats
arc cosinus
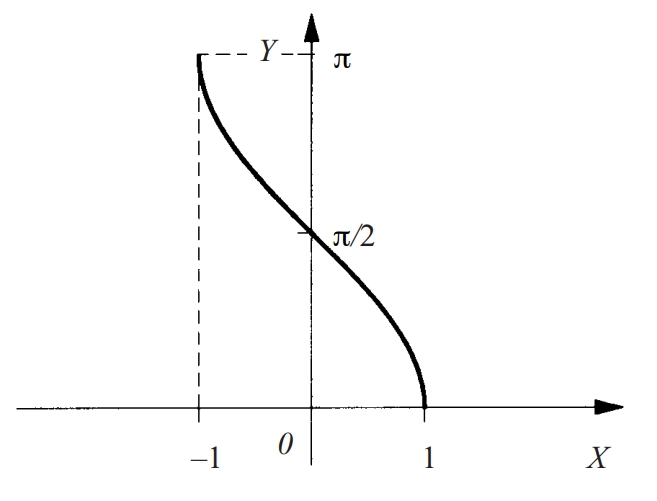
arc cosinus
funció cosinus
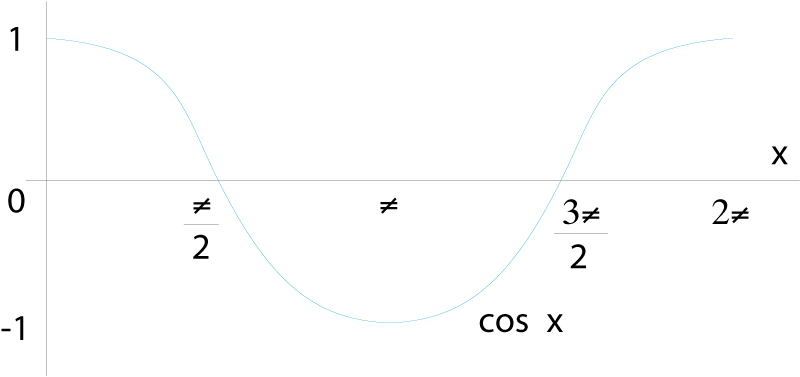
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
cosinus φ
Electrònica i informàtica
En un corrent altern, cosinus de l’angle de desfasament φ entre la tensió i la intensitat.
És abreujat cosφ En el cas de corrents sinusoidals, el cosφ és el factor de potència i depèn del tipus de càrrega
cosinus directors
Matemàtiques
Donada una recta, cosinus dels angles que aquesta recta forma amb els eixos de coordenades del sistema de referència.
funció cosinus hiperbòlic
Matemàtiques
Funció ch:ℝ→ℝdefinida per l’assignació x →ch x, on ch x és el cosinus hiperbòlic del nombre real x.
funció cosinus complex
Matemàtiques
Funció cos: ℂ→ℂdefinida per l’assignació z →(eiz + e-iz)/2.
És una de les sis funcions trigonomètriques complexes
cosinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x
i y
, i un segment de longitud unitat OP
que forma un angle α amb l’eix d’abscisses x
, valor de la projecció de OP
sobre l’eix x
.
Aquesta projecció és el cosinus de l’angle α i és denotada per cos α El cosinus de l’angle α determinat entre dos segments qualsevol és el cosinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al cosinus d’un angle són cosα+β=cosα cosβ-sinα sinβ cos-α= cosα cosαcosβ = cosα+β+cosα-β/2 cosα + cosβ = 2 cosα + β/2cosα - β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α + sin 2 α = 1
funció cosinus hiperbòlic complex
Matemàtiques
Funció ch: ℂ→ℂdefinida per l’assignació z →(ez + e-z)/2, on ez és la funció exponencial complexa.
Se satisfà que ch z = cos iz i que cos z = ch iz , on cos és la funció cosinus complex
cosinus hiperbòlic d’un nombre real
Matemàtiques
Donat un nombre real x
, real ch (x)
definit per ch( x
) =
(e x
+ e - x
)/2
.