Resultats de la cerca
Es mostren 26 resultats
espai d’Euclides
Matemàtiques
Espai vectorial de dimensió finita n en el qual hi ha definida una distància donada per la fórmula (x1,...,xn) i (y1,...,yn) essent les coordenades dels punts x i y.
Els espais euclidians clàssics són els ℝ n la recta, el pla, l’espai, etc
axioma de la paral·lela
Matemàtiques
Axioma segons el qual per un punt exterior a una recta només es pot traçar una única recta paral·lela a la primera.
L’axioma de la parallela resulta equivalent al cinquè postulat d’Euclides i la seva no-inclusió en el sistema axiomàtic euclidià portà a la descoberta de les geometries no euclidianes
àlgebra de Lie
Matemàtiques
Estructura algèbrica consistent en una àlgebra E dotada d’una operació interna, sovint anomenada parèntesi de Lie, (x,y) →[x,y].
Satisfà les següents propietats x,y =0, per a tot x∈E, aquesta segona expressió és la identitat de Jacobi , L’espai euclidià, ℝ 3 , dotat del producte vectorial, té estructura d’àlgebra de Lie Tot grup de Lie té associada una àlgebra de Lie aquestes són, doncs, emprades per a estudiar els grups de Lie
paràmetre de desceleració còsmica
Astronomia
Paràmetre que indica el ritme de variació temporal de l’expansió de l’Univers com a conseqüència de la gravitació del conjunt.
En termes del factor còsmic d’escala R té l’expressió q 0 = -R d 2 R /dt 2 / dR /dt 2 Els diferents valors de q 0 corresponen als diferents models d'Univers q 0 < 1 / 2 corresponen a un Univers obert expansió contínua, q 0 > 1 / 2 corresponen a un Univers tancat collapse final en un temps finit, i q 0 = 1 / 2 correspon a un Univers infinit i un espai euclidià
varietat diferenciable
Matemàtiques
Espai topològic separat V en el qual hi ha definida una família de funcions reals ℱ = ℱ(V).
Aquestes funcions reals compleixen les següents condicions si f és una funció V → ℝ tal, que per a tot punt p de V existeix una funció q de ℱ que coincideix amb en un cert entorn de p , aleshores f és de ℱ si f 1 , , f K són funcions de ℱ, i si F és una funció diferenciable qualsevol sobre l’espai euclidià ℝ k , aleshores F f 1 , , f n pertany a ℱ per a tot punt p de V existeixen funcions f 1 , , f n de F tals, que l’aplicació q → f 1 q , , f n q dóna un homeomorfisme entre un cert entorn U de p un obert de ℝ n Tota funció f de ℱcoincideix sobre U amb F f 1 , , f n , on F és una…
espai topològic
Matemàtiques
Conjunt X en el qual s’ha donat una topologia
.
Els conjunts de la família donada són anomenats oberts , i llurs complementaris, tancats Rep el nom d' entorn obert d’un punt tot conjunt obert que el conté Base de l’espai topològic és una família de conjunts oberts que per reunió poden donar qualsevol altre obert Alguns espais topològics tenen llur topologia definida per mitjà d’una distància, la qual determina la base d’oberts de la topologia formada per les boles o esferes En són exemples la recta real ℝ i els espais euclidians de dimensions superiors ℝ n Un subespai d’un espai topològic és una part de l’espai amb la topologia induïda…
cònica
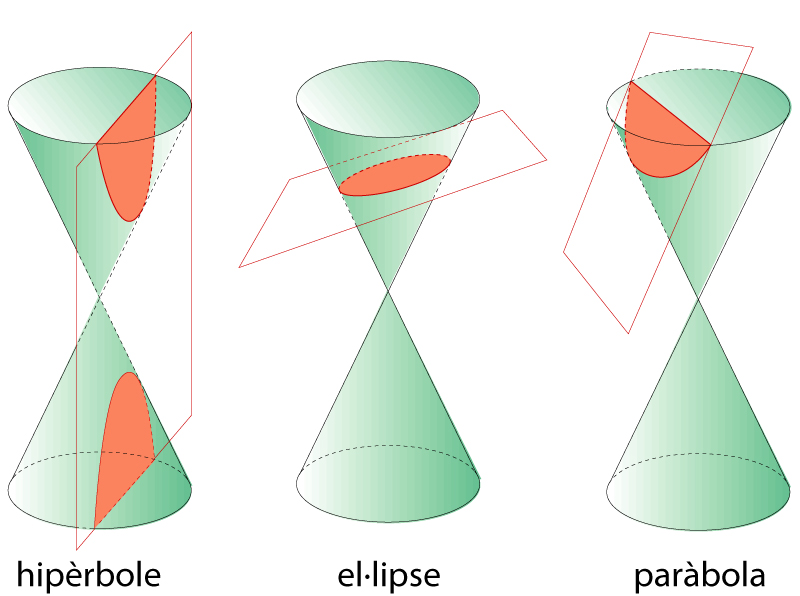
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
equipol·lència
Matemàtiques
Relació d’equivalència entre vectors fixos de l’espai euclidià.
Dos vectors són equipollents si existeix una translació que transforma l’un en l’altre Les classes de vectors equipollents són anomenades vectors lliures vector
Jordi Cerdà i Geberès
Cinematografia
Artista i cineasta amateur.
Vida A partir del 1968 estudià disseny i interiorisme, antropologia i història de l’art, estètica i composició, pintura i gravat Professor d’arts plàstiques, es dedicà a la pintura, la fotografia, el fotomuntatge, la manipulació de suports plàstics, el ready-made , la performance , el trompe-l’oeil , etc , i ha exposat des del 1971 sense interrupció Com a cineasta amateur rodà des del 1968 una vintena de cintes breus o "accions filmades" en formats de pas estret, sol o amb la collaboració de Guillem Baiget, Ricard Solà i Joan Mostaza, un collectiu que estigué actiu fins el 1983 Són reflexions…