Resultats de la cerca
Es mostren 19 resultats
convergència quadràtica
Matemàtiques
Convergència de variables aleatòries que tenen moment de segon ordre finit ( variància finita: E(|x2|) + ∞) i que és caracteritzada per la distància en mitjana quadràtica .
És a dir, que x n convergeix en mitjana quadràtica a x si d x n , x tendeix a zero quan tendeix a infinit Aquesta convergència implica la convergència en probabilitat, però no la quasi-segura
equació quadràtica
Matemàtiques
Equació de segon grau ax2 + bx + c = 0, o, en forma reduïda, x2 + px + q = 0.
Una equació quadràtica pura és la de la forma ax 2 + b = 0 En ax 2 + bx + c = 0, la fórmula de la solució és la quantitat b 2 - 4ac és anomenada discriminant
forma quadràtica
Matemàtiques
Polinomi homogeni de segon grau, o sia
si els valors del polinomi són sempre positius hom diu que la forma és definida positiva, o semidefinida positiva en el cas d’una possible anul·lació per a certs valors de les variables.
quadràtic | quadràtica
mitjana
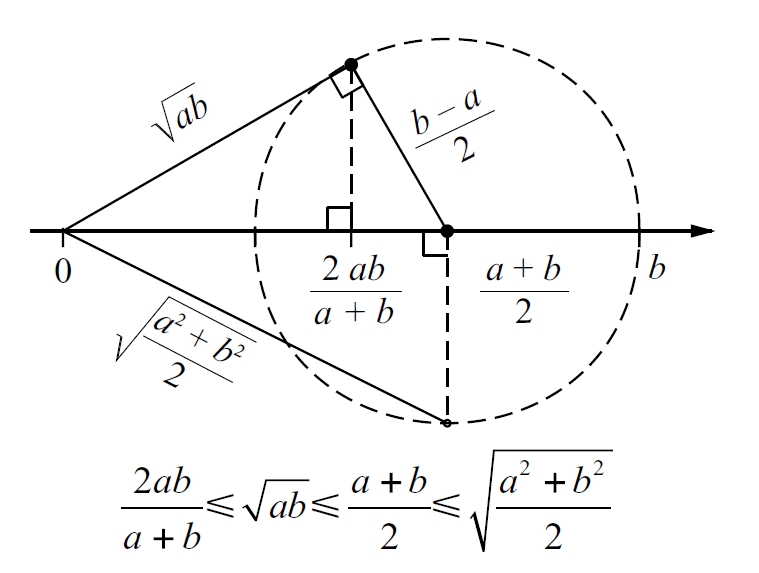
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de la mitjana és…
funció polinòmica
Matemàtiques
Donat un polinomi a0 + a1 X + ... + anXn , funció f(x) que fa l’assignació x → a0 + a1x + ... + anxn.
El grau n del polinomi és el grau de la funció polinòmica Quan n = 2 la funció és quadràtica i quan n = 3 és cúbica
Elwin Bruno Christoffel
Matemàtiques
Matemàtic alemany.
Treballà especialment en el camp de la geometria diferencial Introduí els símbols que duen el seu nom símbols de Christoffel associats a la forma quadràtica gμν, símbols que apareixen en la relativitat general
discriminant
Matemàtiques
Invariant funcional que dóna una relació entre els coeficients d’un polinomi i que permet d’estudiar-ne les arrels i d’altres propietats.
En el cas d’un polinomi de grau n amb una sola variable, a 0 x n + a 1 x n - 1 + + a n , el discriminant és l’expressió En particular, el discriminant d’una equació quadràtica ax 2 + bx + c = 0 té com a expressió Δ = b 2 — 4 ac si Δ > 0, l’equació té dues arrels reals diferents, si Δ=0, té dues arrels reals iguals, i si Δ < 0, no té arrels reals sinó complexes