Resultats de la cerca
Es mostren 38 resultats
Taules trigonomètriques, compàs rígid (Abū’l-Wafā)
Taules trigonomètriques, compàs rígid Abū’l-Wafā
trigonometria

1, circumferència de referència per a la definició de les raons trigonomètriques; 2, representació gràfica de les línies trigonomètriques; 3, símbols emprats en la resuloció de triangles
© fototeca.cat
Matemàtiques
Part de la matemàtica inicialment dedicada a l’estudi de les relacions entre les amplituds dels angles i les longituds dels segments que llurs costats determinen en les rectes que tallen.
La trigonometria es basa en les propietats de les anomenades raons trigonomètriques , que són definides a partir d’un punt P x,y d’una circumferència de centre O i per l’angle α que forma el radi r = OP amb l’eix OX , mitjançant els sis quocients següents sin α = y/r sinus cos α = x/r cosinus tg α = y/x tangent cotg α x/y cotangent sec α = r/x secant cosec α = r/y cosecant Quan el punt P és a una distància r = 1 de l’origen O , el valor absolut d’aquestes raons és representat per la longitud de certs segments anomenats línies trigonomètriques , respectivament,…
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…
línia trigonomètrica
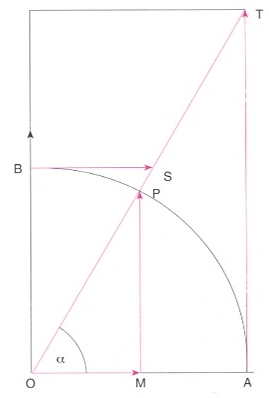
línies trigonomètriques de l’angle α (OA=1); sin α=MP; cos α=OM; tg α=AT; cotg α=BS; sec α=OT; cosec α=OS
© Fototeca.cat
Matemàtiques
Cadascun dels segments amb els quals hom representa geomètricament, basant-se en una circumferència de radi 1 (cercle goniomètric), les funcions trigonomètriques.
funció sinus complex
Matemàtiques
Funció sin: ℂ→ℂdefinida per l’assignació z →(eiz-e-iz)/2i.
És una de les sis funcions trigonomètriques complexes
funció cosinus complex
Matemàtiques
Funció cos: ℂ→ℂdefinida per l’assignació z →(eiz + e-iz)/2.
És una de les sis funcions trigonomètriques complexes
cercle goniomètric
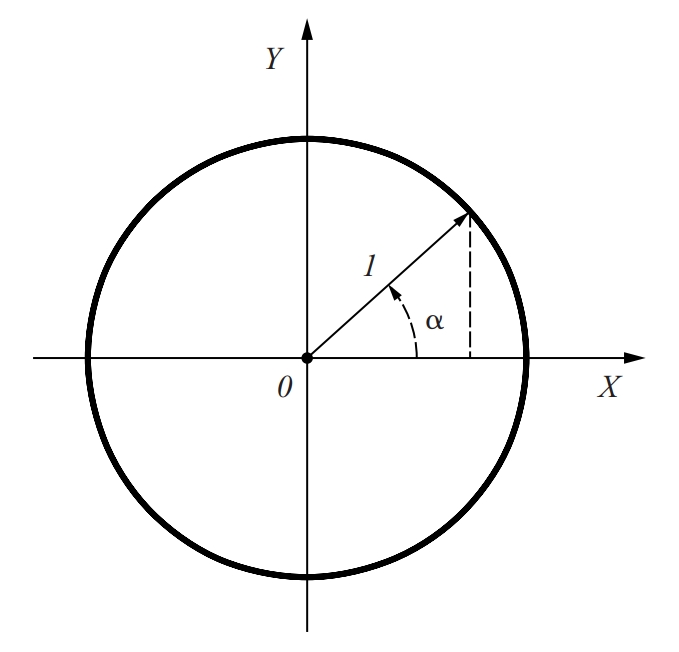
cercle goniomètric
Matemàtiques
Circumferència de radi unitat el centre de la qual és l’origen d’un sistema de coordenades cartesianes (eixos perpendiculars).
És emprat per a definir les raons trigonomètriques d’un angle sinus, cosinus, tangent, etc
funció transcendent
Matemàtiques
Funció que no és algèbrica, és a dir que en el seu desenvolupament en sèrie de potències hi ha un nombre infinit de coeficients no nuls.
En són exemples la funció exponencial, la funció logarítmica, i les funcions trigonomètriques o hiperbòliques
gudermannià
Matemàtiques
Funció Gd: ℝ→(-π/2, π/2) que assigna a un nombre real x el nombre real Gd(x)=arc tg(shx).
Fou usada, originàriament, per a calcular les taules de les funcions hiperbòliques a partir de les taules de les funcions trigonomètriques
