Resultats de la cerca
Es mostren 79 resultats
gauss
Física
Unitat d’inducció magnètica en el sistema CGS electromagnètic.
El seu símbol és Gs Correspon a 1 maxwell per cm 2 i equival a 10 - 4 tesles Rep sel seu nom del matemàtic Carl Friedrich Gauss
Gauss Halvø
Regió de l’amt de Tunu (Grenlàndia).
Carl Friedrich Gauss
Carl Friedrich Gauss
Matemàtiques
Matemàtic alemany.
De família humil, extraordinàriament dotat per a les matemàtiques, pogué rebre ensenyament superior gràcies a la protecció del duc de Brunsvic, que l’envià a la Universitat de Göttingen Director de l’observatori i professor d’astronomia en aquella ciutat, hi residí fins a la mort, dedicat totalment a una fecunda tasca intellectual Els matemàtics li deuen aportacions transcendentals en la teoria dels nombres i en l’àlgebra noció de congruència i notació corresponent, sistematització de l’ús de demostració rigorosa del teorema fonamental de l’àlgebra, teoria de determinants , etc, qüestions…
teorema de Gauss
Física
Matemàtiques
Donat un camp vectorial A, per a tota regió de l’espai de volum V limitada per una superfície S, es compleix que: ∫∫sA·dS = ∫∫∫vdivA dV.
El primer terme de l’equació és el flux de A a través de S És anomenat també teorema de la divergència o d’Ostrogadskij En el cas d’un camp elèctric E , el teorema de Gauss pren la forma q essent-hi la càrrega total dins la regió limitada per S, i ε, la constant dialèctica del medi En el cas d’un camp magnètic B , el teorema de Gauss diu cosa que implica la inseparabilitat dels pols magnètics
campana de Gauss
Matemàtiques
Corba que té per equació cartesiana
.
En estadística representa la funció de distribució normal o de Gauss
enter de Gauss
Matemàtiques
Nombre complex de la forma a + bi, a i b essent-hi enters i .
El conjunt d’enters de Gauss, ℤ i , té estructura d’anell amb unitat
zona de Gauss
Física
Regió tan pròxima a l’eix òptic, que hom hi pot substituir els sinus i les tangents dels arcs pels mateixos arcs.
És anomenada també zona paraxial
pla d’Argand-Gauss
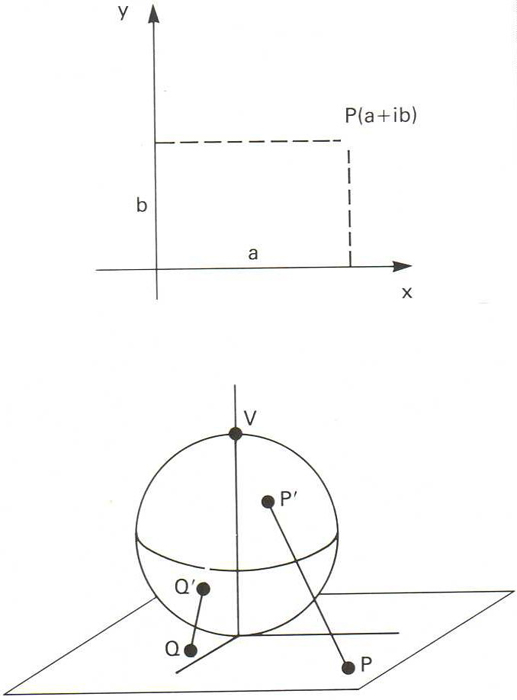
Representació del pla d’Argand-Gauss
© fototeca.cat
Matemàtiques
Pla on ha estat establert un sistema de coordenades cartesianes i en el qual és representat cada nombre complex a + bi per mitjà del punt de coordenades (a, b).
En aquesta representació tots els punts que tenen una o totes dues coordenades infinites són considerats com un mateix punt Per a fer intuïtiu el fet de considerar com un sol tots aquests punts hom utiliza la projecció estereogràfica del pla d’Argand-Gauss sobre una esfera tangent a l’origen de coordenades, de manera que tots els punts de l’infinit del pla van a parar al punt V de l’esfera
nombre primer de Gauss
Matemàtiques
Cadascun dels nombres primers que poden ésser expressats per la fórmula 22n + 1.
Gauss els emprà en estudiar les possibles divisions del cercle, i arribà a la conclusió que hom pot construir amb regle i compàs tot polígon regular amb un nombre primer 2 2 n + 1 de costats
projecció conforme de Gauss
Cartografia
Projecció transversal de Mercator en què els meridians de tangència són el de Greenwich i el situat a 180°.
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Pàgina següent
- Última pàgina