El nombre d’or i l’art
-
- Home
-
- 18 of 32
Què és art?
Socialment, sovint, ens plantegem què considerem que és art.
La paraula art deriva del llatí ars o artis, i el Diccionari de la llengua catalana de l’IEC la defineix com a "destresa, habilitat", però també com a "sistema de regles i preceptes per a fer bé alguna cosa". En altres llengües la definició coincideix. Segons la Real Academia Española (RAE) l'art (arte en castellà) és "virtud, disposición y habilidad para hacer algo", i també és "conjunto de preceptos y reglas para hacer bien algo".
A la Grècia antiga s’incloïa sis coneixements dins l'art: arquitectura, dansa, escultura, música, pintura i poesia. A la societat actual s'ha passat a considerar-ne d'altres; per exemple, s'acostuma a dir que el cinema és el setè art. També s'hi consideren, actualment, altres habilitats i coneixements com podria ser la fotografia.
Però què en pensen i en pensaven els artistes? Creien que l'art és bellesa? En què coincidien els antics pensadors i els més cotitzats artistes del segle passat i de l'actualitat sobre què és bell?
Si seguim llegint la definició d’art, veiem que també s'esmenta aquest aspecte: "aplicació de l'habilitat i del gust de la producció d'una obra segons principis estètics".
Si parlem d’estètica, d’art, de matemàtiques, de proporcions, de bellesa, és de sentit comú que parlem de l’anomenat nombre d’or i tot allò que l’envolta. Ell és el culpable de tot l’embolic. Per això, serà el protagonista d’aquest article.
El nombre d’or i el concepte de bellesa
Tradicionalment el nombre d’or està associat al concepte de bellesa, en el sentit que els objectes on es respecta el nombre d'or semblen més “bonics”, ens “atrauen” més i són més “harmoniosos”.
Us proposo un exercici. Observeu la següent seqüència de rectangles i escolliu el que us sembli més “bonic” i més “harmoniós”.
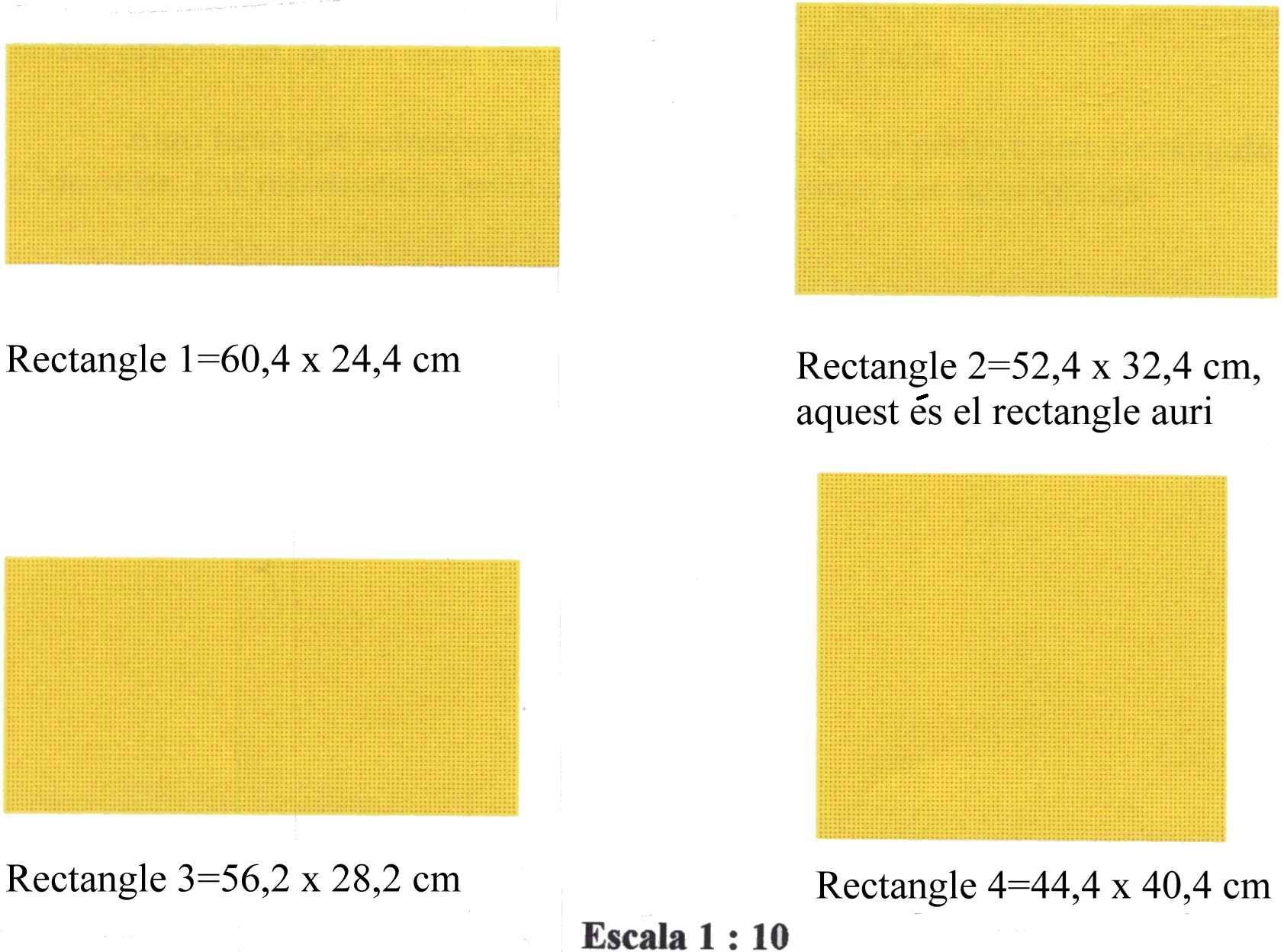
La majoria de vegades que s’ha proposat aquesta experiència, el rectangle escollit ha estat el segon. I per què? Si efectuem la divisió entre la mesura del costat “llarg” i el que mesura el costat “petit” el resultat que s’obté és 1,6180..., és a dir, el valor del nombre d’or. Els rectangles que mantenen aquesta proporció s’anomenen rectangles àurics.
Com podem imaginar, aquest fet no és casual. Els humans tenim una mena d’intuïció per fixar-nos en les formes belles i harmonioses.
Com es pot construir un rectangle àuric?
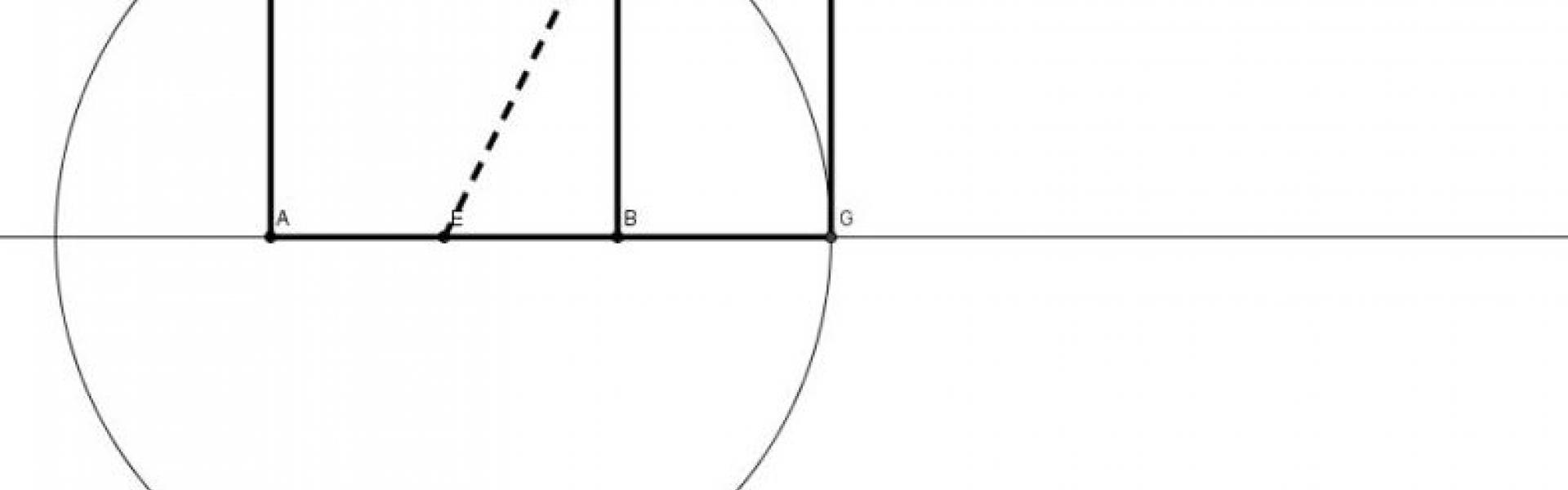
Considerem un quadrat de vèrtexs A, B, C i D que mesuri a unitats de costat, tal com mostra la figura:
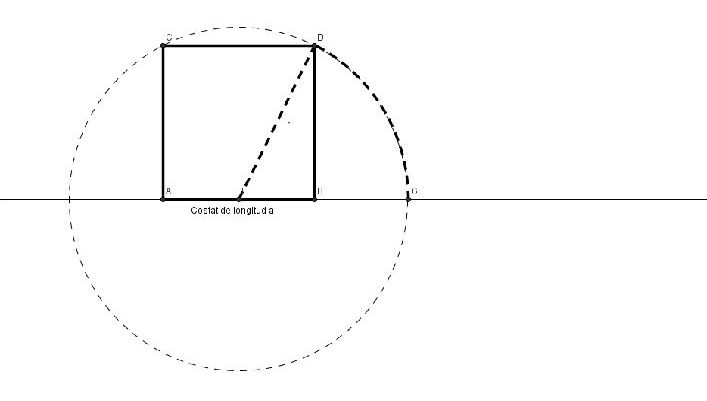
Anomenem E el punt mitjà del costat AB i r el segment que uneix E i el vèrtex D. Aleshores construïm la circumferència de centre E i radi r. Allarguem el costat AB fins a trobar el punt d’intersecció de la circumferència construïda amb la prolongació del costat AB; a aquest punt li diem G. Amb aquests elements podem construir el rectangle que mostrem a la figura:
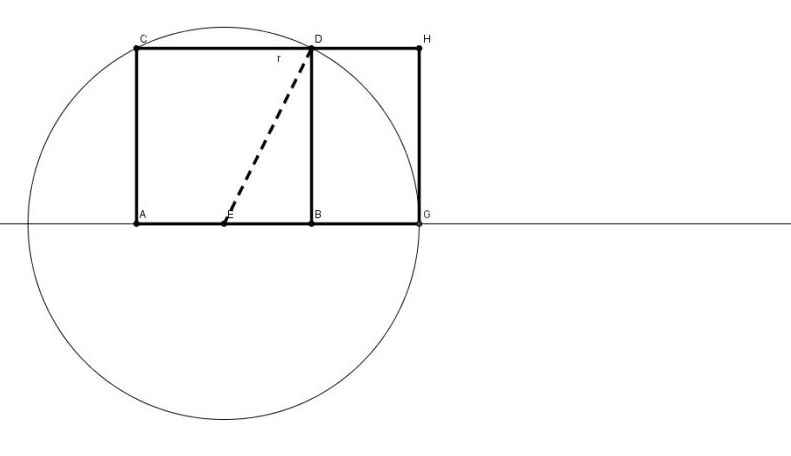
Ens interessa calcular el valor que s’obté de dividir la longitud de la base entre l’alçària, és a dir:
Per calcular GH, cal recordar que AB = a i per tant GH = a (recordem que ABCD és un quadrat cada costat del qual mesura a unitats).
Per trobar el valor AG, hem de considerar que AG = AE + EG =, per a això ens cal determinar el valor de r.
A la figura s’observa que EB mesura i que BD mesura a; llavors per determinar el valor del segment r, aplicarem el teorema de Pitàgores:
Aleshores,
Amb això tenim que el costat “llarg” AG mesura AG = =
Per tant, =
=
.
Aquest fet ens mostra que, efectivament, el rectangle construït és àuric.
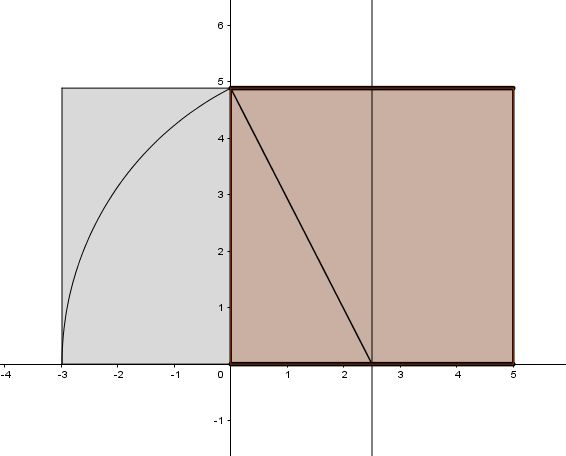
Amb el programari lliure Geogebra, que hom pot descarregar, així es representa gràficament la construcció del rectangle àuric:
On trobem el nombre d’or a l'art?
Els artistes de la Grècia antiga ja varen utilitzar la secció àuria per aconseguir equilibri i bellesa, com podem comprovar en la Venus de Mil.
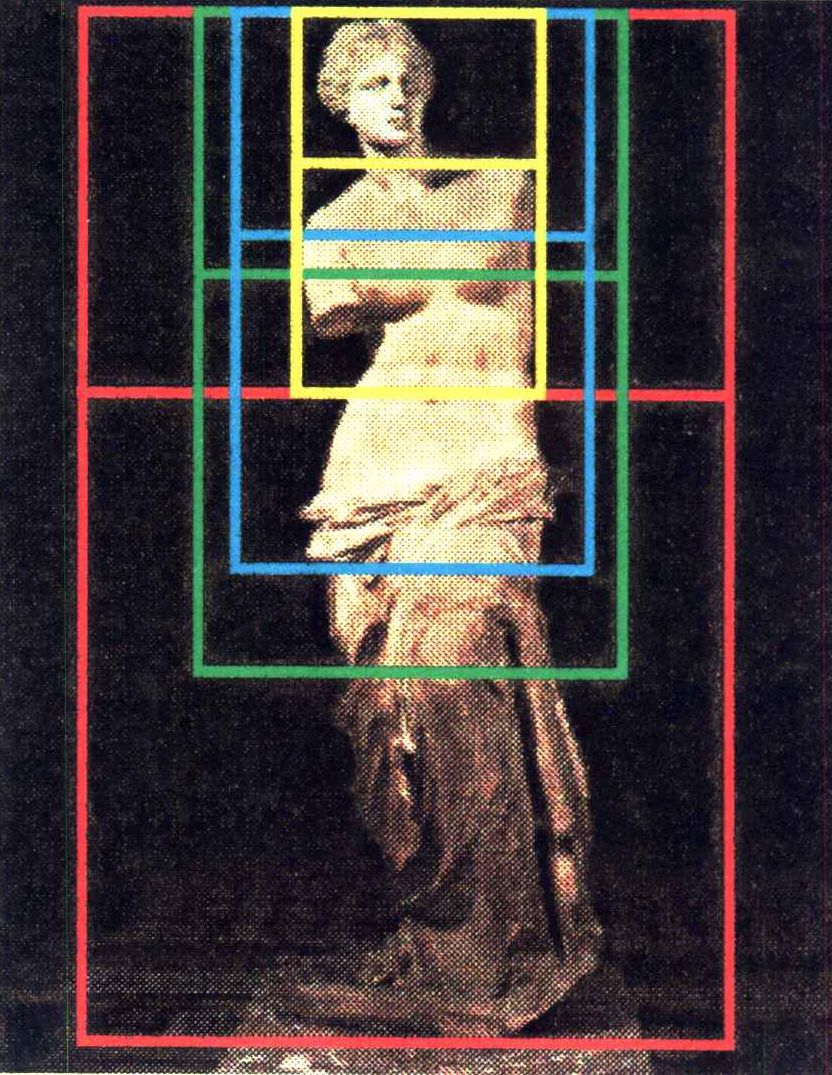
Venus de Mil
Al Renaixement, Leonardo da Vinci, en el seu quadre de La Gioconda (o Mona Lisa) també va utilitzar rectangles àurics per plasmar la figura, inclús el mateix rostre s’emmarca en un rectangle àuric.
A L’home de Vitruvi, Leonardo igualment va proporcionar la figura humana dins de diversos rectangles àurics.
De fet, Leonardo da Vinci va usar el nombre d’or per definir totes les proporcions fonamentals de la seva pintura. En el seu quadre L’últim sopar la proporció àuria apareix en les dimensions de la taula i en les proporcions de les parets i les finestres.
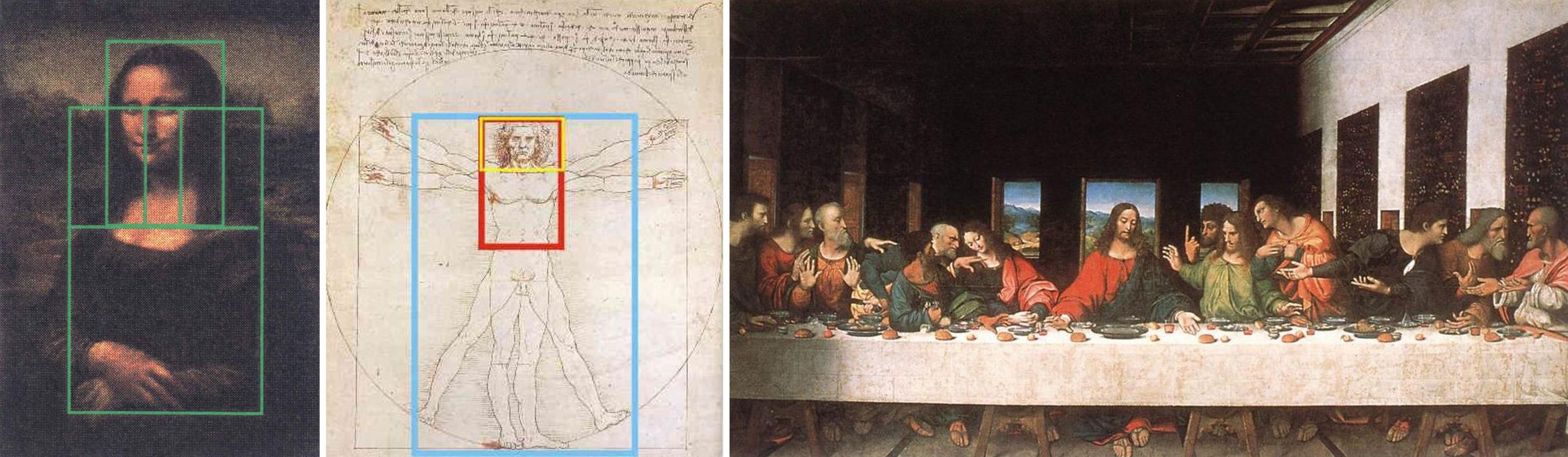
D'esquerra a dreta: La Gioconda, L’home de Vitruvi i L’últim sopar de Leonardo da Vinci
El nombre auri ha interessat també alguns artistes contemporanis, com ara Salvador Dalí, que el va aplicar en diverses obres: Leda atòmica (1949) i Semitassa gegant voladora (1932-1935).
En arquitectura descobrim la utilització del nombre d’or a l’edifici del Secretariat de les Nacions Unides, a la catedral de Notre-Dame de París, al Partenó...

D'esquerra a dreta: Secretariat de les Nacions Unides, catedral de Notre-Dame de París i Partenó
I fins i tot, el nombre d’or ha arribat a la poesia. El mateix Rafael Alberti va escriure un poema (A la divina proporción) dedicat a la proporció àuria:
A la divina proporción
A ti, maravillosa disciplina,
media, extrema razón de la hermosura,
que claramente acata la clausura
viva en la malla de tu ley divina.
A ti, cárcel feliz de la retina,
áurea sección, celeste cuadratura,
misteriosa fontana de mesura
que el Universo armónico origina.
A ti, mar de los sueños, angulares,
flor de las cinco formas regulares,
dodecaedro azul, arco sonoro.
Luces por alas un compás ardiente.
Tu canto es una esfera transparente.
A ti, divina proporción de oro.
I on més el trobem en el nostre entorn?
La presència del nombre d’or a la societat és molt subtil, però a la vegada molt present.
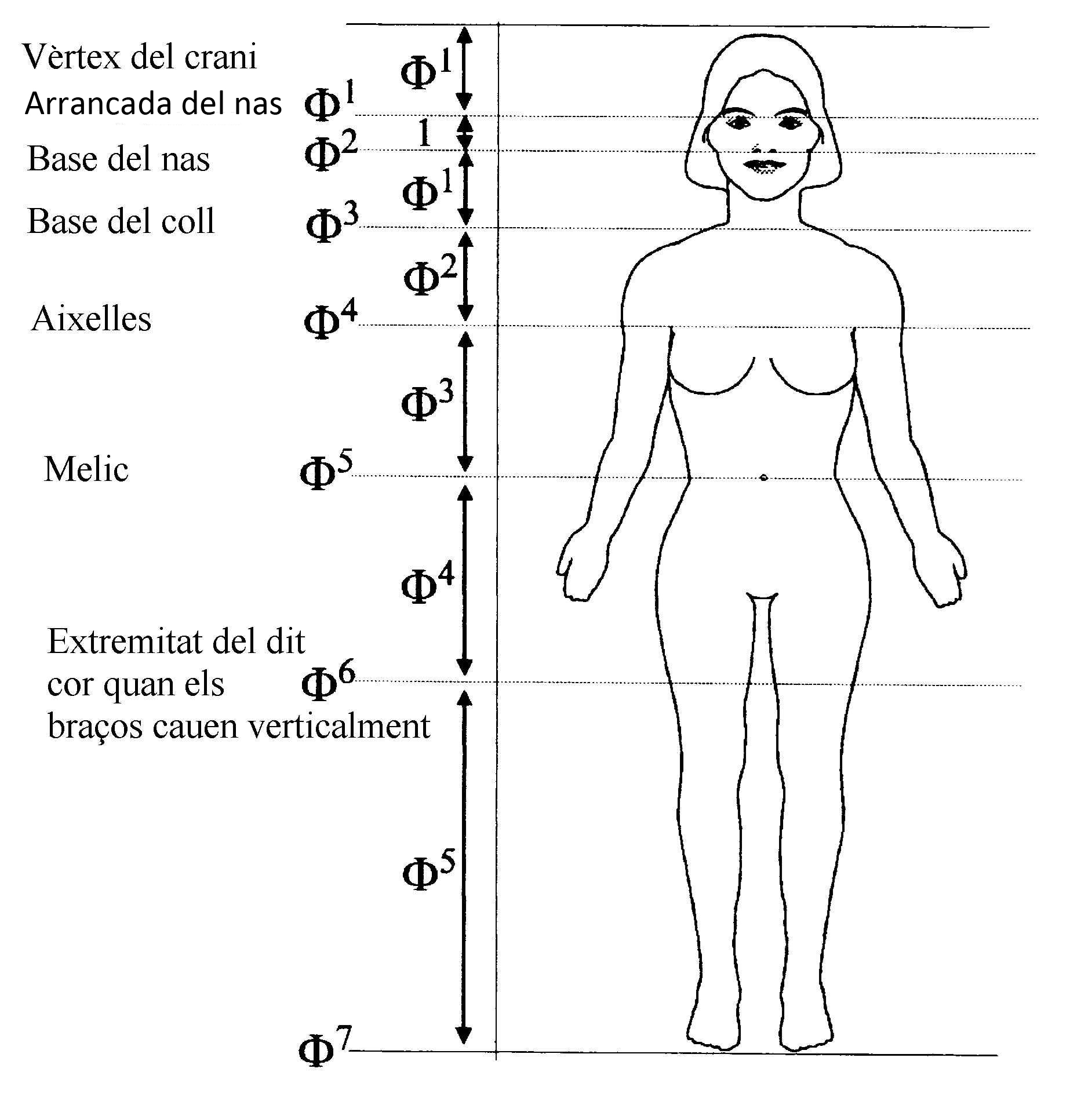
Per exemple, trobem el nombre d’or a la natura. L’alçària del llombrígol és 1,6 vegades el seu diàmetre. També en les proporcions dels dits de les mans, i fins i tot en un ou de gallina!
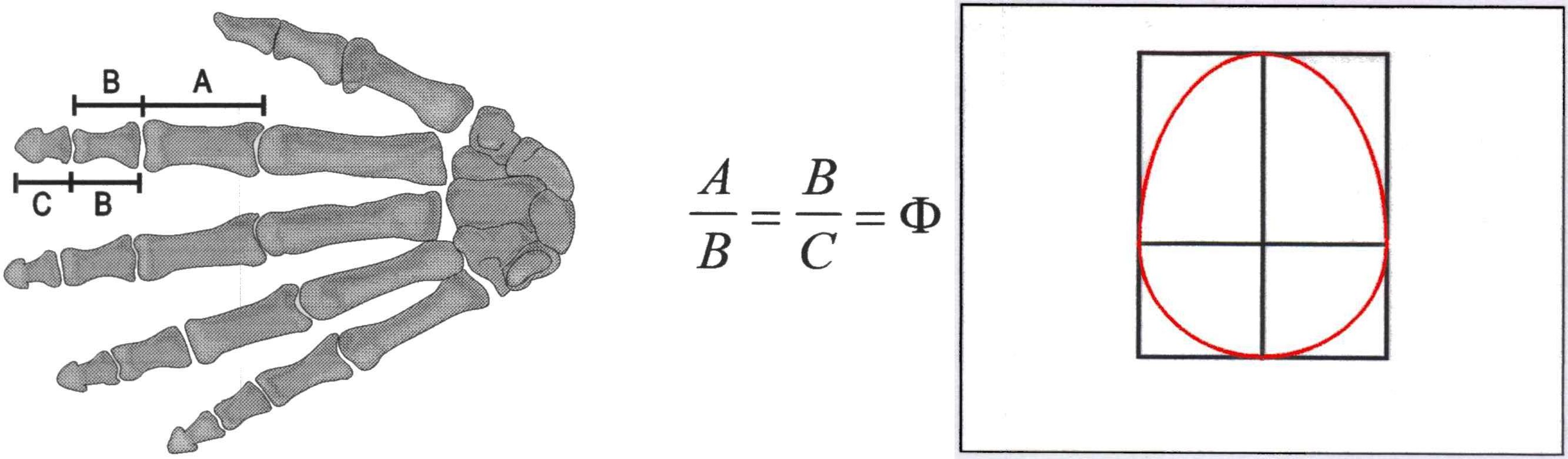
El trobem també en coses quotidianes que hi ha a les nostres butxaques. Si ens entretenim a dividir el costat llarg pel petit dels documents d’identitat, dels paquets de tabac o de les targetes de crèdit obtindrem el nombre d’or.

I també en els camps esportius de futbol, rugbi o hoquei, on descobrirem que en la majoria també trobem el rectangle àuric.
També és extraordinari observar com els sommeliers en els seus tastos de vins usen la proporció àuria en l’harmonia de l’alçària del vi que està distribuït en una copa. L’alçària de la copa dividida per l’alçària del vi s’aproxima al nombre d’or.

Si ens fixem en les tanques publicitàries, notaren que moltes mantenen la relació àuria perquè els professionals de la publicitat pensen que efectivament aquests rectangles són els més harmoniosos i per tant els que el possible client mirarà més.
Inclús Apple, en la seva icona del núvol (icloud) per emmagatzemar dades utilitza la proporció àuria.

Per acabar, parlaré d’una curiositat recent d’utilitat domèstica on hi ha implicada la proporció àurica.
A la IX Fira d’Invents Galàctica de Vilanova i la Geltrú (2001) va ser guardonat l’estenedor Drymax, de la catedràtica de Matemàtiques de l'IES Francesc Macià de Cornellà de Llobregat, Pepita Panadés. Una de les característiques d’aquest estenedor és que, a més a més de minimitzar l’espai que ocupa i de maximitzar el temps d’eixugada, les articulacions estan en proporció àuria.

Si algun dia veieu en algun balcó un estenedor com el Drymax, us convido a contemplar la bellesa d’allò que té alguna cosa a veure amb el nombre d’or.