Eppur si muove (part II): La física dels terratrèmols
-
- Home
-
- 2 of 3
La tragèdia de Turquia ha fet aflorar la qüestió que es repeteix després de cada terratrèmol que sacseja àrees densament poblades: Per què no podem predir els terratrèmols?
Com en moltes altres àrees científiques, gairebé tot el coneixement sobre els terratrèmols l'hem après durant el darrer segle. I no n’hem après poca cosa. Tenim àrees temàtiques especialitzades en la mecànica dels sòlids i fluids de l’escorça, que ens expliquen tant el comportament de les falles a l’escala geològica com a l’escala de les roques que la conformen. Hem après a escoltar les ones sísmiques i a interpretar la informació que ens aporten sobre les propietats físiques de cadascuna de les capes que constitueixen la geosfera. Tenim dades, gairebé a temps real, provinents de la lectura de centenars d’estacions sismogràfiques interconnectades que ens permeten tenir una visió global de l’activitat sísmica al conjunt del planeta. Comptem amb mesures per satèl·lit que ens permeten detectar deformacions mil·limètriques a qualsevol punt de la superfície terrestre emergida. I, com en els casos de Guimerà i Antioquia exposats a la Part I, hem après a llegir el registre històric, arqueològic, i inclús geològic, per estudiar terratrèmols succeïts milers d’anys abans de disposar de tota aquesta tecnologia.
De fet, durant aquest darrer segle hem avançat tant en la ciència dels terratrèmols com ho hem fet en la ciència de l’atmosfera. És evident, en canvi, que disposem de prediccions meteorològiques prou fiables per planificar les nostres decisions quotidianes i per evitar situacions de perill sota condicions atmosfèriques extremes, però no tenim cap pronòstic equivalent sobre “el temps” que farà sota els nostres peus. No podem predir quan, on, ni de quina magnitud serà el proper terratrèmol.
I no només no els podem predir, sinó que des de fa una trentena d’anys en sabem el perquè. Aquesta explicació comença molt abans, a principis del segle xx, amb l’adveniment de dues teories que, pot semblar, poc tenen a veure l'una amb l’altra.
El model mecànic de rebot elàstic
Darrere dels terratrèmols no s’hi amaga cap llei exòtica de la física. No es tracta de fenòmens que involucrin energies relativistes ni efectes quàntics. Des d’un punt de vista reduccionista, la física newtoniana és suficient per entendre la mecànica dels terratrèmols.
A principis de segle xx, el geofísic americà Henry Fielding Reid partí d’aquesta base per desenvolupar la teoria del rebot elàstic, un model simplificat que pretén explicar la fenomenologia dels terratrèmols a partir d'un simple problema mecànic. Observant la deformació i el trencament d'unes tanques durant el terratrèmol de San Francisco del 1906, Reid arribà a la conclusió que els terratrèmols eren les conseqüències de fenòmens de fractura o fricció deguts a esforços de cisalla.

A la imatge, deformacions del terreny observades aquest febrer a Turquia, unes de semblants serviren a H. F. Reid per desenvolupar la teoria del rebot elàstic.
L'esquema conceptual d'H.F. Reid representa el moviment de les falles com el desplaçament d'un bloc que reposa sobre una superfície plana i que és estirat per una molla elàstica. Mentre la tensió de la molla sigui petita, la fricció serà prou alta per retenir el bloc encallat en una posició estàtica. Però si estirem la molla a poc a poc, arribarà un moment en què la força elàstica acumulada, l’esforç tectònic sobre la falla, superi la fricció, i el bloc entrarà en un règim dinàmic que, en poc temps, alliberarà bona part de l’energia elàstica de la molla.
Hom pot imaginar el model del rebot elàstic com un moble que decidim arrossegar per moure’l de lloc. Al principi ens costa de desencallar-lo però, un cop està en moviment, costa menys esforç desplaçar-lo, mentre fem vibrar el terra amb un soroll eixordador. Aquest soroll seria l’equivalent a les ones sísmiques que són la font principal dels danys causats pel terratrèmol.
Per posar un exemple, podem considerar que el ritme de càrrega de les forces tectòniques no han canviat significativament durant el llarg registre històric de terratrèmols a Antioquia. Resolent el senzill problema de mecànica que ens planteja el model del rebot elàstic, hom esperaria que els cicles de càrrega i descàrrega de la falla fossin regulars. I així, podríem predir, de forma senzilla, quan falta per al següent terratrèmol i com serà de gran tan sols coneixent, per exemple, la mida i data dels dos darrers. Hom podria imaginar que petites incerteses en la fricció i la velocitat de càrrega poden distorsionar aquesta periodicitat en introduir petites variacions que no afectarien gaire un règim quasi periòdic de terratrèmols característics. Per tant, no seria un error de mesura tan greu si encara fóssim capaços d'anticipar un terratrèmol amb una precisió de dies amb anys d’anticipació.
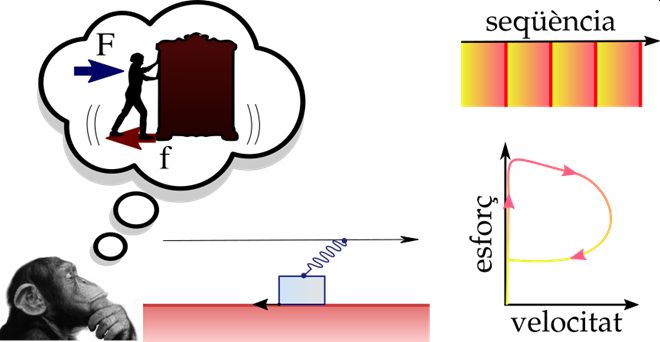
La teoria del rebot elàstic és interpretada de forma diferent en funció del nombre d’elements que consideri el model. Si considerem un sol bloc, estem davant d’un sistema newtonià determinista que genera cicles regulars de terratrèmols que es repeteixen cada cert interval de temps. El podem representar com un sistema dinàmic amb les variables d’esforç i velocitat, reproduint una seqüència regular de càrregues lentes i descàrregues ràpides (els terratrèmols).
Malauradament, els terratrèmols no es comporten com prediu el model d'H.F. Reid. El registre històric ens mostra com els terratrèmols d’Antioquia no segueixen, ni de bon tros, un patró regular. Hi ha èpoques de gran intensitat, com el segle vi, seguit de segles sense registres, forts terratrèmols ocasionals o doblets sobtats com el d’aquest mes de febrer. El model d'H. F. Reid és molt atractiu com a explicació qualitativa als terratrèmols, però la seva visió reduccionista és insuficient per reproduir l'estadística dels terratrèmols o per fer cap mena de predicció.
De la mecànica determinista al caos
Mentre H.F. Reid presentava el seu model de terratrèmols, els matemàtics Henri Poincaré i Ivar Otto Bendixson plantejaren unes idees que canviarien la ciència en un futur no gaire llunyà. S’adonaven que un sistema dinàmic de tres o més variables podia evolucionar de manera “estranya”, diferent del comportament predictible que, com provaren, s’ha de complir en un sistema de dues variables quan aquestes són contínues i derivables. Aquest principi, que pot semblar abstracte, és una de les bases del que, als anys 60, es definí com a teoria del caos: el descobriment que, en determinats sistemes dinàmics que anomenem no lineals, petites variacions en les condicions inicials poden portar a solucions divergents i pràcticament imprevisibles en temps relativament curts.
I què té a veure això amb el model d'H.F. Reid?
El model de rebot elàstic és, precisament, un d’aquests sistemes dinàmics no lineals, però constituït per només dues variables independents. Per exemple, el podem representar a partir de la velocitat de desplaçament del bloc i la tensió de la molla que el subjecta. Per tant, el model de rebot elàstic és determinista i té solucions regulars, tal com esperarien H. Poincaré i I. O. Bendixson. Però aquesta aproximació de la falla com un sol element sòlid és molt agosarada. L’escorça terrestre és un sistema complex, constituït per moltes parts i de moltes mides diferents que interactuen mecànicament entre si.
Suposem, per exemple, que modelem una falla com un sistema de dos blocs, en comptes d’un, desplaçant-se sobre la mateixa superfície. Cada bloc és sotmès a un mateix esforç tectònic, però ara hi incorporem una força elàstica addicional connectant els dos blocs, i associem a cada un una massa i/o un coeficient de fricció diferent de l’altre. Ara tenim un sistema dinàmic molt semblant a l’anterior, però amb quatre graus de llibertat: la velocitat dels dos blocs i la tensió de les dues molles.
El resultat és un sistema caòtic on, en comptes de cicles tancats, trobem solucions obertes que divergeixen molt ràpidament si considerem petites variacions en les condicions inicials. A efectes pràctics, en comptes de tenir una seqüència regular de terratrèmols, trobem seqüències molt irregulars. A vegades salta un bloc i d’altres salten els dos. A vegades els salts són menuts i d’altres són gegants. A vegades són molt seguits i d'altres estan separats per temps molt llargs. Aquesta dinàmica ja s’assembla molt més al que observem en la seqüència històrica d’Antioquia.
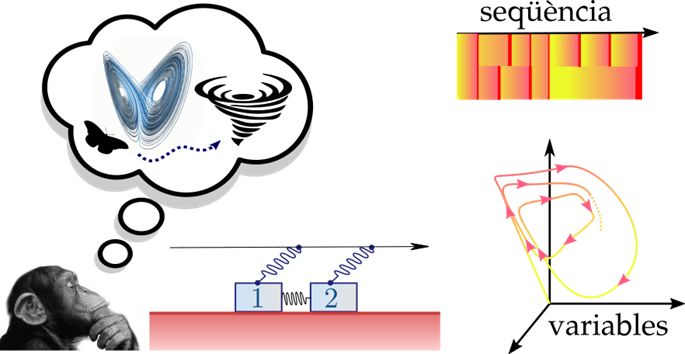
Considerant un model de rebot elàstic amb dos blocs, obtenim un sistema caòtic determinista. Si en coneixem amb molta precisió els detalls físics, podem estimar l’evolució del sistema dinàmic, fer pronòstic a molt curt termini però que fallen molt ràpidament a mesura que ens allunyem en el temps. En aquest cas, la seqüència de càrregues i descàrregues és irregular, així com el nombre de blocs que es desplacen a cada descàrrega.
Del caos a la física estadística
Si fóssim capaços de modelar els sistemes de falles com a sistemes de dos o, fins i tot, més blocs, tindríem eines matemàtiques per predir terratrèmols, almenys a curt termini. Es tractaria d’un problema semblant al plantejat en la meteorologia.
Precisament, els límits temporals de la predicció meteorològica és una de les qüestions que va originar la teoria del caos als anys 60 del segle passat amb els treballs del matemàtic americà Edward Norton Lorenz i el famós efecte papallona. Avui en dia, gràcies a multitud de fonts de dades, tenim informació global i molt precisa dels paràmetres que defineixen el sistema dinàmic atmosfèric. I, tot i així, és pràcticament impossible predir el temps a més de dues setmanes vista, tot i emprar potents supercomputadores per a la tasca.
El cas dels terratrèmols és encara més dramàtic.
Per començar la informació que tenim de l’estat, composició i esforç de l’escorça terrestre i les forces induïdes des del mantell és molt limitada. Tota la informació local que podem obtenir és a partir de perforacions molt puntuals, o el sondatge del subsol amb ones sísmiques naturals o induïdes. Tant és el nostre desconeixement que sovint ignorem l’existència d’una falla activa fins que no causa un terratrèmol, perquè els temps de retorn són més llargs que el nostre registre sismogràfic.
Aquest fet no seria tan greu si no fos per una propietat fonamental de la física dels sistemes complexos, presentada pel físic teòric Per Bak l’any 1987: la criticalitat autoorganitzada, de la qual haurem de parlar en publicacions futures. Tot el que ens cal saber, per ara, és que, tan aviat fou descoberta, tant Per Bak com molt altres investigadors coetanis,[1] s’adonaren que els terratrèmols són fenòmens crítics i que presenten invariància d’escala.
Per un cantó, la invariància d’escala vol dir que no podem associar una “mida” característica al voltant de la qual es distribueixin les “mides” de terratrèmols que observem. Per cada terratrèmol gran en tenim molts més de petits, i si canviem l’escala d’observació veurem repetit exactament el mateix patró. Aquesta llei estadística és coneguda com a llei de Gutenberg-Richter en el cas concret dels terratrèmols. En conseqüència, no podem associar una regió amb un risc de terratrèmols d’una magnitud determinada, sinó, tan sols, amb un temps de recurrència que esperem per a cada magnitud segons l’activitat sísmica de la regió.
Per altra banda, la criticalitat també implica que, inclús un cop ha començat el terratrèmol, és molt difícil predir quanta energia acabarà alliberant, o si vindran rèpliques encara més fortes. Aquesta és l’aportació més crucial de la teoria de la criticalitat autoorganitzada pel que fa a la possibilitat de predir de terratrèmols. Seguint el símil meteorològic, seria com si un núvol petit de tempesta del qual ho sabem gairebé tot pogués eixugar-se sense causar pluja o, tot el contrari, créixer fins a un huracà de categoria 5 en pocs minuts, i no tinguéssim cap manera d’anticipar-ho.
La condició de criticalitat dels terratrèmols ens posa en la situació més precària possible a l’hora de fer-ne pronòstic. Però, a la vegada, ens obre la porta a entendre el problema des del marc de la mecànica estadística, on tenim tota una teoria sobre l’origen i les conseqüències dels fenòmens crítics.
La mecànica estadística és la ciència que permet descriure sistemes constituïts per un nombre molt alt, tendint a infinit, d’elements que interactuen entre si. En aquesta aproximació és impossible de predir l’instant i la magnitud d’un terratrèmol, però sí que ens permet definir un seguit de lleis estadístiques, com poden ser les freqüències amb les quals ocorren terratrèmols d’una certa magnitud, és a dir, la llei de Gutenberg-Ritcher, i com es relacionen amb les propietats geomecàniques d’una falla o regió. Per fer-ho hem desenvolupat eines matemàtiques molt semblants a les que emprem per entendre com les propietats termodinàmiques d’una substància, com pot ser la temperatura, pressió i volum, depenen del nombre, moviment i interaccions entre les partícules que la constitueixen. Aquestes lleis estadístiques donen nom a una branca de la geofísica que nomenem sismologia estadística.
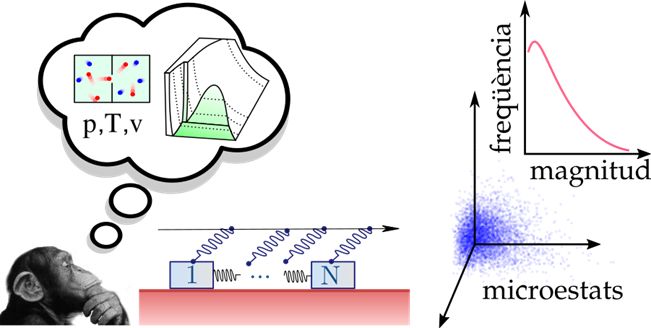
Si considerem el model de rebot elàstic amb un nombre N gran de blocs, podem tractar el sistema amb les eines de la mecànica estadística i, en comptes de pronòstics a curt termini, tindrem lleis estadístiques estacionàries que s’ajusten molt bé a les observacions a llarg termini.
Si, efectivament, la teoria de la criticalitat autoorganitzada és una aproximació vàlida al fenomen dels terratrèmols, aquests són intrínsecament impredictibles. La manca de predicció no és per manca d’informació, o d’un model escaient, sinó una conseqüència inevitable dels processos naturals d’autoorganització cap al punt crític on les falles són sempre a prop de lliscar de manera invariant d’escala. Sabem que aquesta falta de predictibilitat és certa, com a mínim, dins del marc teòric que ens permet entendre els terratrèmols en l'àmbit estadístic i l’únic que, a hores d’ara, ens permet donar resposta a les observacions a gran escala que ens podrien servir per fer pronòstic. No podem descartar que aquesta aproximació teòrica sigui només això, una aproximació, i que existeixi, en paraules del sismòleg Tom Jordan, una "bala de plata" amagada, en forma de mesura capaç de predir els terratrèmols. Però no podem fiar la nostra seguretat, ni desviar masses dels nostres recursos, a la cerca d’un greal del qual dubtem de l’existència.
Per acabar, la nostra incapacitat de predir terratrèmols no vol dir que estiguem indefensos. Tot el coneixement acumulat durant aquests anys de recerca ens permet prendre diverses mesures per preparar-nos i reduir riscos quan aquests succeeixen. En el proper article veurem què podem fer, i què no, avui dia, per fer front als perills sísmics.
BIBLIOGRAFIA[1]
Bak, P., and Tang, C. (1989). “Earthquakes as a self‐organized critical phenomenon”. Journal of Geophysical Research: Solid Earth, 94(B11), 15635-15637.
Olami, Z., Feder, H. J. S., and Christensen, K. (1992). “Self-organized criticality in a continuous, nonconservative cellular automaton modeling earthquakes”. Physical review letters, 68(8), 1244;
Rundle, J. B., and W. Klein, “Scaling and critical phenomena in a cellular automaton slider block model for earthquakes”, J. Stat. Phys., 72, 405–412, 1993.
PER SABER-NE MÉS:
Correig i Blanchar, Antoni. "Ocurrència i predicció de terratrèmols". Revista de física, 1999, Núm. 17, p. 24-31.
Bak, Per. How nature works: the science of self-organized criticality. Springer Science & Business Media, 2013.
Buchanan, Mark. Ubiquity: the science of history, or why the world is simpler than we think. (2000).