Nombres amigables
-
- Home
-
- 3 of 32
Avui parlaré dels nombres amigables (algunes fonts també en diuen nombres amics), i per fer-ho partiré d’un exemple.
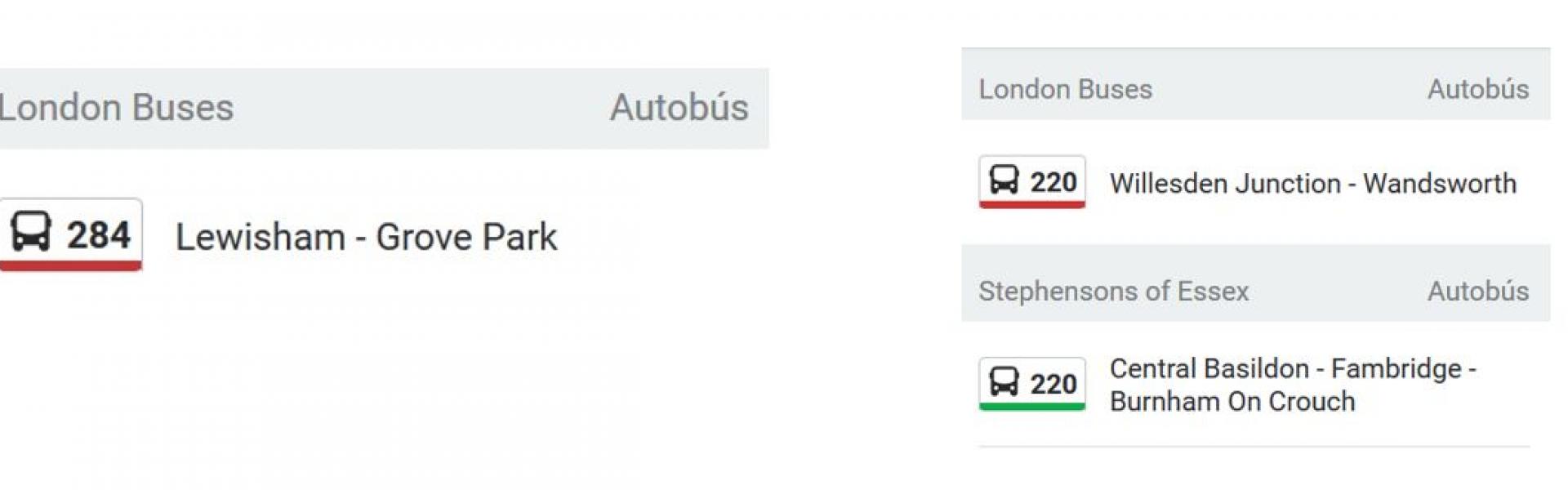
La figura 1 ens mostra la numeració d’unes línies del transport urbà de la ciutat de Londres, i probablement us pregunteu: per què ha triat aquestes línies? quina relació hi ha entre els nombres indicatius de cada línia?
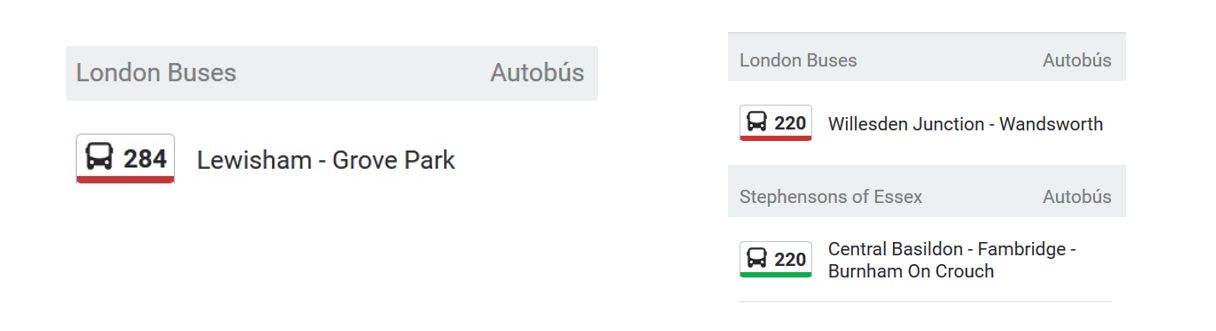
Figura 1. Imatge de les línies d’autobusos de Londres.
Vegem-ho. Si prenem el nombre 220 i calculem els seus divisors, excepte ell mateix, o divisors propis, tenim el resultat següent: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 i 110. Si després els sumem (1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110), n’obtenim el nombre 284.
Com podem observar, la suma no és precisament 220, de manera que podem afirmar que el 220 no és un nombre perfecte.
Arribats aquí, si fem les mateixes operacions amb el 284, els seus divisors propis són 1, 2, 4, 71 i 142, i sumant-los obtenim el nombre 220.
D’una manera sorprenent, la suma dels divisors d’un dels nombres és l’altre nombre, i recíprocament. Aquestes parelles de nombres que compleixen que la suma dels divisors propis d’un d’ells és igual a l’altre nombre, i viceversa, s’anomenen nombres amigables. Formalment podem que dir dos nombres naturals x i y es diuen amigables si la suma dels divisors propis de x és igual a y i viceversa.
Es coneixen moltes parelles de nombres amigables, algunes d’elles amb nombres força grans, però la parella 220 i 284 ha protagonitzat nombroses referències al llarg de la història. Per exemple, se sap d’una creença medieval que deia que si es donava de menjar a dues persones al mateix temps, però no en el mateix lloc, amb aliments que contenien una inscripció de 220 per a una i de 284 per a l’altra, aquestes dues persones es feien amigues per “art de màgia”.
Una altra curiositat que té com a protagonista la parella de nombres amigables 220 i 284, és una llegenda que comparteixo literalment a continuació: “Explica una llegenda que hi havia un sultà aficionat als puzles que, en descobrir que tenia un matemàtic com a presoner, va decidir plantejar-li la següent qüestió. El sultà va dir al matemàtic que li proposés un repte, un problema, i que seria lliure durant el temps que necessités per resoldre’l. Però, un cop resolt pel sultà, el matemàtic seria executat. El matemàtic li va explicar que els nombres 220 i 284 són nombres amigables i li va plantejar el repte de trobar una altra parella de nombres amigables. El sultà no ho va aconseguir, i el matemàtic va morir de vell i essent un home lliure”.
Finalment, al segle XIV, ibn Khaldun (1332 – 1406) al llibre Muqaddima (1377) escriu: “Les persones expertes en els talismans afirmen que els nombres amigables 220 i 284 exerceixen una forta influència per establir una unió o una amistat molt forta entre dues persones”.

Figura 2. Anells hexagonals, amb or groc i or rosa, amb la parella de nombres amigables 220 i 284, de la botiga londinenca Comford Station. La caixa conté una explicació sobre què és una parella de nombres amigables.
Quantes parelles de nombres amigables coneixem?
El primer exemple de parella de nombres amigables, precisament el 220 i el 284, va ser mencionat per Pitàgores (569 aC – 475 aC).
Cap a l’any 850, l’astrònom i matemàtic àrab Ṯābit ibn Qurra (826 – 901) va descobrir una fórmula que generava nombres amigables a partir dels valors p, q i r calculats així:
p = 3 · 2n-1 - 1
q = 3 · 2n - 1
r =9 · 22n-1 - 1
de manera que n>1 és un nombre enter i p, q i r són nombres primers. Sota aquestes condicions, el parell definit com a = 2n· p · q i b =2n · r són nombres amigables. Aquest resultat es coneix com la regla de Ṯābit.
D’aquesta manera, per n = 2, 4 i 7 es generen tres parells de nombres amigables:
| 22 · 5·11 = 220; | 22· 71 = 284 |
| 24 · 23 · 47 = 17.296; | 24 · 1.151 = 18.416 |
| 27 · 191 · 383 = 9.363.584; | 27 · 73.727 = 9.437.056 |
Resumit a la taula:
|
n |
p |
q |
r |
2npq |
2nr |
| 2 | 5 | 11 | 71 | 220 | 284 |
| 4 | 23 | 47 | 1.151 | 17.296 | 18.416 |
| 7 | 191 | 383 | 73.727 | 9.363.584 | 9.437.056 |
S’ha comprovat que, per a valors n ≤ 191.600, no es genera cap altra parella de nombres amigables. D’altra banda, cal destacar que no totes les parelles de nombres amigables s’obtenen d’aquesta manera; per exemple, les parelles 1.184 i 1.210, d’una banda, i 6.232 i 6.368, de l’altra, no es generen amb aquesta fórmula.
Tot i que en el món àrab es coneixien altres parelles de nombres amigables, en realitat, en el món occidental, fins al segle XVII només se'n coneixia una (220 i 284). L’any 1636, Pierre Simon de Fermat (1601 – 1665) va descobrir que el 17.296 i el 18.416 també eren amigables. Un parell d’anys més tard, Descartes (1596 – 1650) va trobar una nova parella: 9.363.584 i 9.437.056. El 1747, L. Euler (1707 – 1783) va proporcionar un llistat amb 64 parelles de nombres amigables. Com a anècdota, destaca el fet que en la llista no es trobaven els nombres 1.184 i 1210, una parella de nombres amigables descoberta més d’un segle després, l’any 1866, per Niccolò Paganini, un jove estudiant italià de16 anys.
El mateix Euler va trobar una nova regla per generar nombres amigables, que diu així:
“Si k i n son nombres naturals tals que k ≤ n i els tres nombres p, q i r obtinguts com:
p = (2k + 1)2n+1-k - 1
q = (2k + 1)2n+1 - 1
r = (2k + 1)222n+2-k - 1
són nombres primers, aleshores 2n+1 · p · q i 2n+1 · r són una parella de nombres amigables”. Per k=1 s’obté la regla de Ṯābit.
Hi ha algunes afirmacions sobre els nombres amigables que encara no s’han demostrat, i que, per tant, encara són conjectures:
- En cada parella de nombres amigables, tots dos nombres tenen la mateixa paritat.
- Tots els nombres amigables imparells són múltiples de 3.
- Tots els nombres amigables parells compleixen que la suma dels seus dígits és un múltiple de 9.
Actualment, amb l’ajuda de potents ordinadors, s’han trobat al voltant de 7.500 parelles de nombres amigables, però encara desconeixem si hi ha infinits parells de nombres amigables.