Nombres primers i RSA

D'esquerra a dreta, Adi Shamir, Ron Rivest i Len Adleman

A mitjans de l’any 1970, Ron Rivest, Adi Shamir i Len Adleman, tots tres investigadors del Massachusetts Institute of Technology (MIT), van dissenyar un enginyós mètode per enviar missatges encriptats, l’anomenat RSA (acrònim del nom dels científics mencionats). Aquest mètode es basa en descompondre o factoritzar un nombre com a producte de dos nombres primers.

En un primer moment es podria pensar que descobrir el codi d’encriptació és una tasca senzilla utilitzant el mètode de “prova i error”, perquè recordem que un nombre primer és aquell que només és divisible per 1 i per ell mateix. Però en realitat no ho és, de senzilla, perquè l’RSA es basa a utilitzar nombres primers molt grans.

Clau digital de seguretat RSA SecurID SID700 sense connector USB

Existeixen mètodes eficients per trobar nombres primers molt grans (al voltant de 400 dígits) i per multiplicar-los entre si, però ningú coneix un algoritme eficient per factoritzar grans nombres (de l’ordre de 1.000 dígits). Per exemple, trobar dos números primers que multiplicats tenen com a resultat 35 és senzill (7 per 5), però si busquem dos nombres primers que el resultat de multiplicar-los sigui 455.020.999, ja és molt més laboriós.

El sistema RSA va ser mencionat per primera vegada, entre el gran públic, l’agost del 1977. A la revista Scientific American, Martin Gadner va escriure a la secció de passatemps matemàtics —una secció en la qual va escriure entre el 1952 i el 2000— l’article “Un nou tipus de xifra que costaria milions d’anys desxifrar”, en el qual llançava un desafiament als lectors: descodificar un text xifrat en què la clau per aconseguir-ho consistia a factoritzar el nombre

n = 114.381.625.757.888.867.669.235.779.976.146.612.010.218.296.721.242.362.562.561.842.935.706.935.706.935.245.733.897.830.597.123.563.958.705.058.989.075.147.599.290.026.879.543.541

com a producte de dos nombres primers p i q, els quals s’usaven per a la descodificació.

El premi era de 100 dòlars, una xifra molt suculenta l’any 1977, i es demanava als lectors d’enviar la solució al laboratori d’informàtica del MIT. Els artífexs del sistema RSA (Rivest, Shamir i Adleman) van rebre més de tres mil respostes, però cap de correcta!

La resposta bona la va rebre el MIT el 26 d’abril de 1994, disset anys després del desafiament, i es va aconseguir gràcies a la col·laboració de més de 600 persones. Va resultar que n = p · q, en què:

p = 32.769.132.993.266.709.549.961.988.190.834.461.413.177.642.967.992.942.539.798.288.533

q = 3.490.529.510.847.650.949.147.849.619.903.898.133.417.764.638.493.387.843.990.820.577

i que el missatge de text que havia encriptat Martin Gadner el 1977 era: the magic words are squeamish ossifrage (‘les paraules màgiques són trencalòs impressionant’).

Amb tot, queda clar que els nombres primers són clau per a la seguretat de l’RSA perquè trobar dos factors primers d’un nombre molt gran és una tasca extremadament difícil i lenta. En aquests moments s’estan xifrant missatges amb més de 500 dígits, perquè fins i tot als ordinadors més potents se’ls fa difícil factoritzar xifres de tal magnitud. Per tant, si no es troba cap algoritme que permeti factoritzar nombres d’aquesta magnitud podem garantir que el sistema RSA continuarà sent un dels mètodes de xifratge més segurs.

El sistema RSA és el més mediàtic dels denominats de clau pública, i anualment se celebra un congrés exclusiu de RSA (podeu obtenir-ne informació a https://www.rsaconference.com/).

I ara que sabem de la importància del sistema RSA i dels nombres primers, ens podem preguntar, però, com ens afecta aquest fet en el nostre dia a dia? La resposta és molt fàcil. D’ambdós depenen les transaccions comercials per Internet, les comunicacions, les signatures electròniques, els registres en aplicacions, etc.

Per això, conèixer com es distribueixen i descobrir nombres primers cada vegada més grans és important per a la criptografia i tot un repte que va més enllà de les matemàtiques.

En aquest sentit, fa poc hem tingut una molt bona notícia. El mes d’octubre d’aquest 2024, es va saber que el nombre primer més gran conegut és 2^136,279,841 − 1, un número que té 41.024.320 dígits quan s’escriu en base 10. Es va trobar a través d’un ordinador del matemàtic Luke Durant.

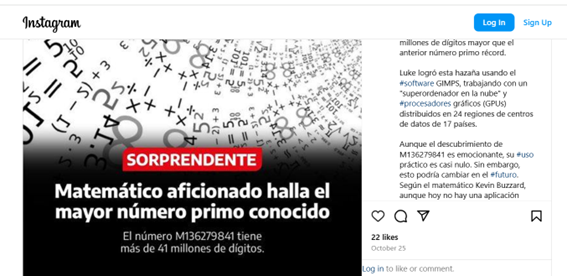
Imatge de text aparegut a Instagram anunciant la troballa del nombre primer més gran conegut

Podem llegir més sobre aquest descobriment a la plataforma Great Internet Mersenne Prime Search (GIMPS), a la notícia del diari Ara (en línia) de l’11 d’octubre de 2024 i també a la seva xarxa social X. Aquest nombre és el 52è primer de Mersenne (llegiu, el meu anterior article “Nombres perfectes, abundants i deficients”).

Si bé els ordinadors quàntics podrien en el futur trencar l’RSA amb l’algoritme anomenat de Shor, l’ús de nombres primers més grans pot retardar aquest risc fins que s’implementin alternatives segures.

En resum, l’ús de nombres primers grans augmenta la robustesa del sistema i allarga la seva vida útil davant tecnologies i tècniques d’atac cada vegada més avançades. Per aquest motiu és una gran notícia la troballa de nombres primers grans.

Foto de capçalera: (CC BY-SA 1.0) Mateusz Adamowski