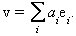Les coordenades (a1,..., an) de v en la base [e1,..., en] són úniques. Tot espai vectorial té una base (és una conseqüència de l’axioma de Zermelo). Si l’espai E té una base formada per un nombre finit d’elements (base finita) l’espai és de dimensió finita; aleshores totes les bases tenen el mateix nombre d’elements, nombre que s’anomena la dimensió de l’espai, dim E. Un espai vectorial de dimensió finita té infinites bases. Dues bases de E, B =[e1,..., en] i B’ =[e’1,..., e’n] es relacionen mitjançant una matriu de canvi de base:
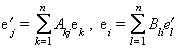
essent
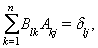
és a dir, les matrius A i B són inverses: B = A-1. La matriu A permet de fer un canvi de base, és a dir, obtenir les coordenades en la base B’ d’un vector qualsevol v a partir de les seves coordenades en la base B:
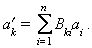
Un espai té dimensió infinita si donat un nombre natural n és possible de trobar-hi n vectors linealment independents. Una base d’un espai de dimensió infinita és un conjunt de vectors, generalment numerable, tal que qualsevol vector de l’espai pot ésser expressat com a combinació lineal finita o infinita (en el sentit d’una sèrie que convergeix segons alguna noció de límit) dels seus elements.