Dit d’una altra manera, cal cercar els anomenats coeficients de regressió a1, a2 , . . . , an, b, tals que facin mínima la distància al quadrat d2 (y, a1 x1 + . . . + an xn +b). Si hom representa els valors de les variables estadístiques en l’espai ℝn + 1 , aleshores l’hiperplà y = a1 x1 + . . . + an xn + b és dit de regressió (per a n = 1, hom té la recta de regressió, i per a n = 2, el pla de regressió). En el cas que n = 1, la recta de regressió y = ax + b té per coeficients
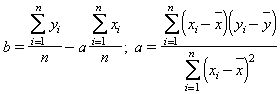
on xi , yi són els valors de les variables, i x, y, les seves esperances o valors mitjans. En el núvol de punts del pla obtingut per la representació dels valors (xi , yi), la recta de regressió és exactament la recta que fa mínima la suma dels quadrats de les distàncies dels punts (xi , yi) als punts de la recta, obtinguts per projecció dels punts (xi , yi) paral·lelament a l’eix Y.