Resultats de la cerca
Es mostren 4981 resultats
pont de Sant Antoni
Art romànic
Pont
Pont romànic de la parròquia de la Maçana, sobre el riu Valira, al camí d’Andorra la Vella a Ordino, a la gorja de la Grella.
Prop hi ha el el santuari de Sant Antoni de la Grella
pont de Rei
Pont
Construcció i obres públiques
Pont internacional damunt la Garona, a la frontera francoespanyola, límit septentrional de la Vall d’Aran.
hort de Pontons
Pont
Construcció i obres públiques
Antiga sumptuosa alqueria del municipi de València, a Patraix, al SW de l’antic nucli urbà, feta construir a la fi del s. XVII pel canonge Antoni Pontons i Garcia (mort a Rubielos Bajos, Aragó, el 1706).
Moltes de les pintures que l’adornaven foren traslladades modernament a la catedral i algunes de les estàtues del jardí de Ponzanelli adornaren posteriorment alguns indrets de la ciutat, com el Tritó a la Glorieta i les Quatre Estacions als Vivers El 1705, essent el canonge Pontons un ardent filipista, la casa fou segrestada i esdevingué dependència reial de Carles III i hi fou condicionada una famosa sala del tron, que es conservà, excepcionalment, fins al s XX Mort Pontons, Felip V n'esdevingué hereu, i després passà a particulars, que la convertiren en fàbrica de seda
pont dels Escalls
Art gòtic
Pont
Pont de construcció medieval a l’antic camí d’Andorra la Vella a Engordany i les Escaldes; al costat hi havia una torre gòtica on fou signat el tractat del pont dels Escalls (1881), que posà fi a la revolta del 1880, punt culminant de les discòrdies entre els partits andorrans.
xarxa
Matemàtiques
Aplicació d’un conjunt dirigit en un conjunt qualsevol, essent un conjunt dirigit un conjunt ordenat segons una relació reflexiva, transitiva i filtrant superiorment.
Tota successió és una xarxa x 1 , x 2 , x 3 , , on el conjunt dirigit utilitzat per a fer l’índex dels elements és el dels nombres naturals En anàlisi, la convergència per xarxes generalitza la seqüencial
matriu wronskiana (de n funcions)
Matemàtiques
Donades n funcions d’una variable real, f1,...,fn, matriu que té a la primera fila les funcions donades, i a les (n—1) files restants, les (n—1) primeres derivades: .
Rep el seu nom del matemàtic J M H Wroński
volta
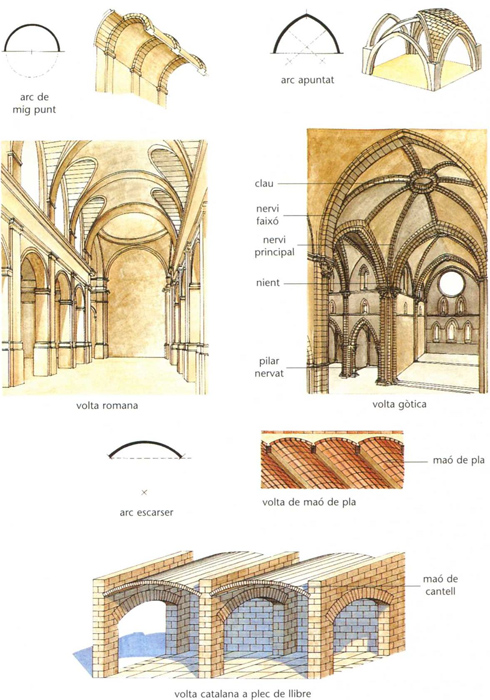
Perfil de l’arc generador, estructura bàsica i exemple constructiu de tres tipus de volta: a dalt, cilíndrica o de mig punt (a l’esquerra) i per aresta gòtica (a la dreta); a baix, escarsera
© Fototeca.cat
Arquitectura
Estructura arquitectònica corbada que cobreix un espai, forma un sostre, sosté una graderia, etc., conformada amb elements que recolzen mútuament i exerceixen una pressió exterior suportada per parets, pilars, etc.
En la seva forma simple , la volta és generada pel moviment directriu d’un arc Segons el perfil d’aquest arc, en resulta una volta cilíndrica o de mig punt , o de canó seguit , o de tartana si l’arc és de mig punt, apuntada o ogival , o en punta d’ametlla si és apuntat, escarsera o escassana , o rebaixada si és escarcer, d’ansa-paner si és carpanell, peraltada si és peraltat, parabòlica si és parabòlic, rampant o d’escala si és rampant, etc Segons el moviment directriu de l’arc en l’espai, es genera una volta recta quan el moviment directriu és perpendicular al seu pla, inclinada o…
variància
Matemàtiques
Mesura de la dispersió d’una variable aleatòria X respecte al seu valor mitjà.
Hom la defineix mitjançant la següent igualtat σ 2 X = E X - E X 2 E X essent l’esperança matemàtica o valor mitjà de X La variància és, doncs, el moment de segon ordre corresponent a la variable X centrada La seva arrel quadrada σ és la desviació tipus En el cas discret, és a dir, si la variable aleatòria X pren un nombre finit de valors x 1 , …, x n amb probabilitats respectives P 1 , …, P n , aleshores hom té
variació d’una funció
Matemàtiques
Donat un interval [a, b], suprem, per a totes les possibles particions de [a, b], de la suma de les oscil·lacions de la funció en tots els subintervals de la partició.
És a dir, si a = x o < x 1 < < x n - 1 < x n = b és una particiò P qualsevol de a, b i | f x i + 1 - f x i | l’oscillació de la funció en un subinterval arbitrari x i , x i + 1 i essent aleshores la variació de f en a, b serà V f = sup { P , P∈ℱ} , on ℱdesigna el conjunt de totes les particions de l’interval a, b Si V f és un nombre finit, hom diu que la funció f té variació fitada en l’interval a, b Tota funció real definida en un interval tancat que s’expressi com a diferència de dues funcions creixents és de variació fitada aquesta propietat caracteritza les…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina