Resultats de la cerca
Es mostren 43 resultats
coordenades generalitzades
Física
Coordenades, generalment no cartesianes, que, en nombre igual al de graus de llibertat d’un sistema mecànic, són escollides per tal de simplificar la forma de les seves equacions dinàmiques.
Defineixen la configuració del sistema, és a dir, són les coordenades de l’espai de configuració
funció de Routh
Física
Per a un sistema de n graus de llibertat, funció donada per la fórmula .
on s i t són enters tals que s + t = n , les q i amb i variant d’1 a s són les coordenades generalitzades que tenen com a moments lineals les p i , les ξ j amb j variant d’1 a t són les coordenades generalitzades per a les quals, pel fet de no tenir un moment lineal fàcilment utilitzable, hom prefereix emprar les coordenades de velocitat generalitzades x j , i L és la funció de Lagrange del sistema Respecte a les coordenades q i , la funció de Routh és anàloga al hamiltonià i respecte a les ξ j , ho és al lagrangià Per tant La funció de…
configuració
Física
Situació d’un sistema físic en la qual queda perfectament especificada la posició de cadascuna de les parts components.
La configuració d’un sistema és donada per les coordenades de cada partícula o bé, en el cas de lligams, per les coordenades generalitzades del sistema, en nombre igual al de graus de llibertat d’aquest En afegir a una configuració q 1 ,,q n els moments canònics conjugats p 1 ,,p n , hom determina totalment l' estat del sistema L' espai de configuració , de coordenades q 1 ,,q n , esdevé així l' espai fàsic , de coordenades q 1 ,,q n , p 1 ,,p n
equacions de Lagrange
Física
Equacions diferencials que descriuen el moviment d’un sistema mecànic.
Donat un sistema de coordenades generalitzades, és a dir, un sistema qualsevol de coordenades q 1 , q 2 , , q n que permeti d’especificar les posicions de les partícules del sistema mecànic, les n equacions de Lagrange, una per a cadascuna de les coordenades generalitzades, són on L és el lagrangià i q i la velocitat generalitzada, és a dir, la derivada respecte al temps de la coordenada q i Les equacions de Lagrange, establertes ja per Euler i anomenades també d’Euler-Lagrange , són, en la major part dels problemes interessants, equivalents a les…
centroide
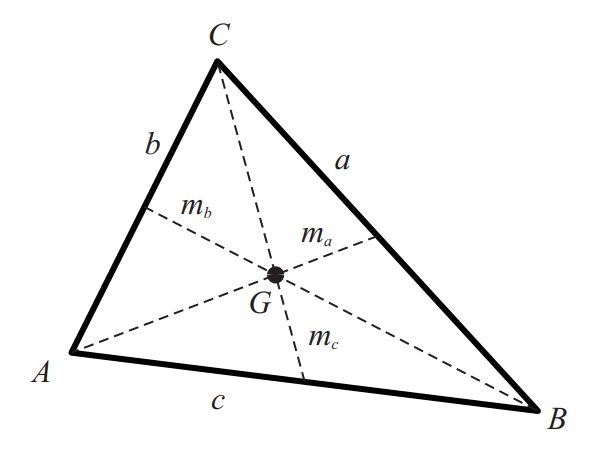
del triangle ABC
Física
Matemàtiques
Punt especial associat a una figura o a una distribució de punts que en el cas físic correspon al centre de massa o de gravetat, de vegades anomenat també baricentre.
En algunes figures el seu centroide és determinat geomètricament Per exemple, en un triangle és el punt d’intersecció de les mitjanes, i en els polígons políedres regulars és el centre de la circumferència esfera circumscrita Donat un conjunt discret de punts x 1 ,, x n amb masses m 1 ,, m n , punt que té per coordenades la mitjana de les coordenades dels punts ponderada per les masses En altres figures es poden trobar per integració les expressions de les coordenades del centroide Així, en figures amb una distribució de massa contínua φ x , el centroide…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…
Julius Plücker
Física
Matemàtiques
Matemàtic i físic alemany.
Fou professor a les universitats de Berlín, Halle i Bonn Féu recerques, juntament amb Hittorf, sobre els gasos enrarits 1865, l’òptica dels cristalls i els espectres de gasos Estudià i analitzà els raigs catòdics i llur desviació pels camps magnètics 1868 És conegut sobretot pels seus treballs en geometria analítica, on introduí una noció original de coordenadescoordenades plückerianes Publicà, entre altres obres, Analytisch-geometrische Entwicklungen 1835, Theorie der algebraischen Kurven 1839 i Neue Geometrie des Raumes 1868
principi de relativitat de Galileu
Física
Principi segons el qual les lleis que governen els fenòmens mecànics en dos sistemes de referència S i S´, proveïts d’un moviment relatiu rectilini i uniforme, tenen la mateixa forma.
Per a comprovar aquest principi, considerat per Galileu com el principi fonamental de la mecànica, cal establir les fórmules de transformació per a passar d’un sistema de referència inercial S anomenat també sistema o eixos de Galileu a un altre S ´ que tingui un moviment rectilini i uniforme respecte al primer En el cas que el sistema S´ de coordenades espaciotemporals x´, y´, z´, t´ es mogui amb velocitat v rectilínia i uniforme, segons l’eix x de S de coordenades espaciotemporals x, y z, t , les fórmules de transformació, anomenades de Galileu , són x´ = x-vt ,…
sistema tricromàtic
Electrònica i informàtica
Física
Sistema per a l’especificació d’un color, basat en la possibilitat de reconstituir-lo mitjançant la mescla additiva de tres components de colors convenientment elegits.
Hom utilitza les anomenades coordenades tricromàtiques o de cromatisme , x, y, z, i un diagrama normalitzat color
principi de D’Alembert
Física
Principi diferencial de la mecànica que permet, mitjançant l’addició de les forces d’inèrcia i les forces aplicades a un sistema, derivar les equacions del moviment d’un sistema no sotmès a forces de fricció i tal que el treball virtual de les forces de lligam s’anul·li.
De l’expressió inicial s’obtenen, en canviar a coordenades generalitzades d’un sistema conservatiu amb lligams holònoms, les equacions de Lagrange