Resultats de la cerca
Es mostren 63 resultats
distribució canònica
Física
Distribució de probabilitat.
Segons aquesta, la probabilitat Pr de trobar un sistema en un estat r d’energia E r és donada per l’expressió Pr ∝ C - β E r , on β = KT - 1 és el paràmetre de temperatura absoluta del focus tèrmic amb el qual és en equilibri el sistema
distribució de Planck
Física
Distribució de probabilitat de trobar els fotons d’una radiació electromagnètica en llurs diversos estats quàntics.
És expresada per on n i és el nombre de fotons que es troben a l’estat i corresponent a la freqüència ν ι , h és la constant de Planck, k és la constant de Boltzmann i T la temperatura absoluta La distribució de Planck és l’aplicació de l' estadística de Bose-Einstein als fotons
distribució de Gibbs
Física
Llei estadística, establerta el 1911, que dóna la probabilitat wnque un cos macroscòpic qualsevol, considerat com una part relativament petita d’un gran sistema aïllat, resti en un estat d’energia En.
És expressada per la fórmula w n = Ae - E n / k T , A essent-hi la constant de normalització obtinguda de la condició Σ w n = 1, T la temperatura absoluta i k la constant de Boltzmann
distribució de Fermi-Dirac
Electrònica i informàtica
Física
Distribució energètica en un sistema de fermió.
La distribució de Fermi-Dirac representa la probabilitat que un determinat nivell d’energia E del sistema estigui ocupat pels fermions, i és donada per l’expressió on k és la constant de Boltzmann, T és la temperatura absoluta i E F és el nivell de Fermi Per a valors d’energia E tals que E > 5kTE F , la distribució de Fermi-Dirac pot ésser substituïda per l’aproximació clàssica donada per la distribució estadística de Boltzmann, f E = exp- E-E F / kT
estadística de Fermi-Dirac
Física
Estadística que regeix la distribució d’un conjunt de fermions en funció dels possibles valors de l’energia i de les posicions.
Té en compte les regles quàntiques, i el principi d’exclusió de Pauli Quan un conjunt de partícules és regit per l’estadística de Fermi-Dirac, la seva funció d’ona total és antisimètrica respecte a l’intercanvi de dues de les partícules és a dir, que canvia de signe sota l’intercanvi de les dues partícules La funció de distribució és la distribució de Fermi-Dirac
centroide
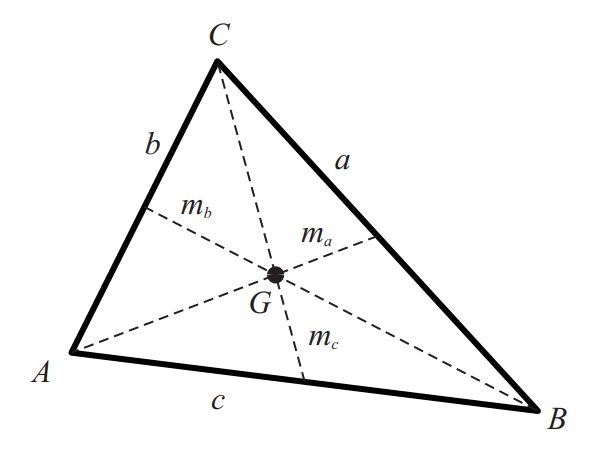
del triangle ABC
Física
Matemàtiques
Punt especial associat a una figura o a una distribució de punts que en el cas físic correspon al centre de massa o de gravetat, de vegades anomenat també baricentre.
En algunes figures el seu centroide és determinat geomètricament Per exemple, en un triangle és el punt d’intersecció de les mitjanes, i en els polígons políedres regulars és el centre de la circumferència esfera circumscrita Donat un conjunt discret de punts x 1 ,, x n amb masses m 1 ,, m n , punt que té per coordenades la mitjana de les coordenades dels punts ponderada per les masses En altres figures es poden trobar per integració les expressions de les coordenades del centroide Així, en figures amb una distribució de massa contínua φ x , el centroide és el punt x̄ = ƒφ x xdx…
moment dipolar
Electrònica i informàtica
Física
Donada una distribució de càrregues elèctriques en repòs, coeficient del terme 1/r2 que apareix en desenvolupar el potencial creat per les càrregues en un punt de l’espai en sèrie de potencies de 1/r
.
Anàlogament, hom anomena moment quadripolar, octopolar , etc, els respectius coeficients dels termes 1/r 3 , 1/r 4 , etc, de la dita sèrie Aquestes magnituds només depenen del sistema de càrregues i, quant a llur significació física, cal dir que el moment dipolar és una mesura de la major o menor coincidència dels centres de càrregues positives i negatives i el moment quadripolar mesura la poca o molta simetria esfèrica de la distribució Un desenvolupament anàleg del potencial vector del camp magnètic dóna lloc als moments dipolars , quadripolars , etc, magnètics , el primer dels…
camp magnetoestàtic
Física
Camp magnètic engendrat per una distribució d’imants permanents en repòs.
Antigament hom considerava que un imant permanent era constituït de masses magnètiques i que, en completa analogia amb la llei de Coulomb de l’electroestàtica, la intensitat del camp magnètic creat per una massa magnètica puntual q m en un punt del buit de vector de posició r era H = q m /4πμ o r / r 3 , on μ o és la permeabilitat del buit i r és el mòdul del vector r la força exercida sobre una altra massa magnètica q' m era aleshores F = q' m H Aquesta aproximació coulombiana a la magnetoestàtica ha estat abandonada, però illustra el fet que el camp magnetoestàtic és conservatiu, i que…
camp electroestàtic
Física
Camp elèctric engendrat per una distribució de càrregues elèctriques en repòs.
La intensitat del camp que crea una càrrega puntual q en un punt de vector de posició r , és la força per unitat de càrrega que experimenta una càrrega puntual q' situada al punt r E = F / q ' De la llei de Coulomb resulta que, al buit, E = q /4πε 0 r / r 3 , on ε 0 és la permitivitat del buit i r és el mòdul del vector r El camp electroestàtic és conservatiu, i deriva del potencial elèctric V E = -grad V
configuració electrònica
Física
Distribució dels electrons d’un àtom o molècula en els diversos orbitals d’aquests.
Per a deduir les configuracions electròniques dels àtoms, hom es basa en el fet que un àtom multielectrònic pot collocar els seus electrons en un conjunt d’orbitals formalment anàleg al de l’àtom d’hidrogen, bo i seguint l’ordre de menor a major energia dels orbitals i tenint en compte el principi d’exclusió L’ordre en què es van emplenant d’electrons els orbitals d’un àtom neutre és 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 6d, ~ 5f orbital atòmic La configuració electrònica d’un àtom és simbolitzada per mitjà de la notació dels orbitals amb un índex volat a la dreta…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Pàgina següent
- Última pàgina