Resultats de la cerca
Es mostren 16 resultats
acceleració d’un punt
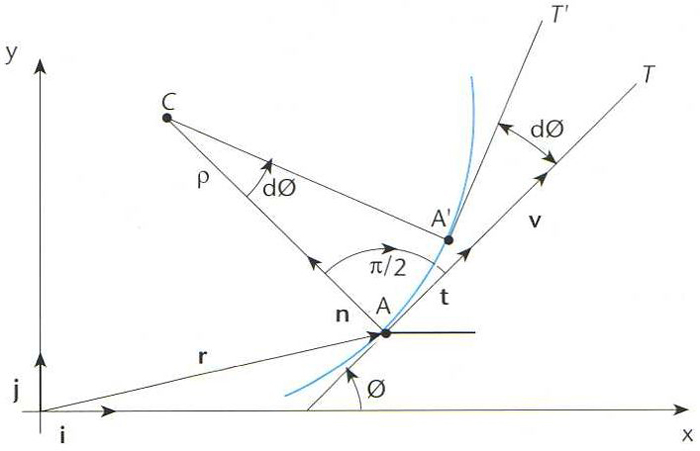
Acceleració d’un punt
© Fototeca.cat
Física
Variació de la velocitat del punt respecte al temps.
En el seu sentit més general és el vector a = < d v /dt , on v és el vector velocitat del punt del fet que v = d r /dt resulta que a = d 2 r /dt 2 , on r és el radi vector La unitat d’acceleració és el m/s 2 En termes dels vectors tangent t i normal n a la trajectòria, a pot escriure’s com a = dv/dt t + v 2 /ρ n , essent ρ el radi de curvatura La primera component és l’ acceleració tangencial és deguda al canvi de valor de la velocitat i la segona és l’ acceleració normal és deguda al canvi de la direcció de la velocitat En el cas…
quantitat de moviment
Física
Per a un punt material de massa m, vector p definit per p=m v, on v és la velocitat del punt material.
És anomenat també moment lineal del punt La seva variació en el temps, d p/ dt , és relacionada amb la resultant R de les forces que actuen sobre el punt mitjançant l’expressió d p/ dt= R Per a un sistema de punts, hom defineix la quantitat de moviment del sistema per Si v G és la velocitat del centre de masses del sistema, aleshores se satisfà que P = M v G , on és la massa total del sistema Si les forces internes que s’exerceixen mútuament els punts del sistema satisfan la llei d’acció i reacció tercera llei de Newton, aleshores la variació temporal de P és igual…
corrent de desplaçament
Física
Tipus de corrent elèctric que té lloc en un material, conductor o aïllant, quan hom hi aplica un camp elèctric variable amb el temps.
Aquest concepte, ideat per Maxwell, és aplicat especialment en el cas dels dielèctrics, on el corrent de desplaçament és molt superior al de conducció La densitat de corrent de desplaçament és donada per j D =/ dt , on D és el desplaçament elèctric atès que D =ε o E + P , resulta que j D =ε o d E / dt + d
vida mitjana
Física
Valor mitjà del temps d’existència (és a dir, de ‘‘vida’’) d’un nucli d’una espècie radioactiva abans de desintegrar-se.
La constant de desintegració λ de l’espècie és λ = dn/n dt , on dn és el nombre de nuclis desintegrats en l’interval dt quan hi havia n nuclis hom pot demostrar que la vida mitjana τ és τ = 1/λ La vida mitjana τ és relacionada amb el període de semidesintegració o semivida T de l’espècie per la relació τ = T/ ln2
capacitat calorífica
Física
En sentit ampli, quantitat de calor necessària per a augmentar en un grau la temperatura d’un cos.
En un sentit més rigorós, relació dQ/dT entre l’energia calorífica dQ lliurada a un sistema i l’augment de temperatura dT , quan aquesta darrera tendeix a zero, sempre que no tinguin lloc canvis de fase o reaccions químiques Si la massa del sistema és un gram, la capacitat calorífica rep el nom de calor específica si és un mol, calor molar, i si és un àtom gram, calor atòmica
llei de les àrees
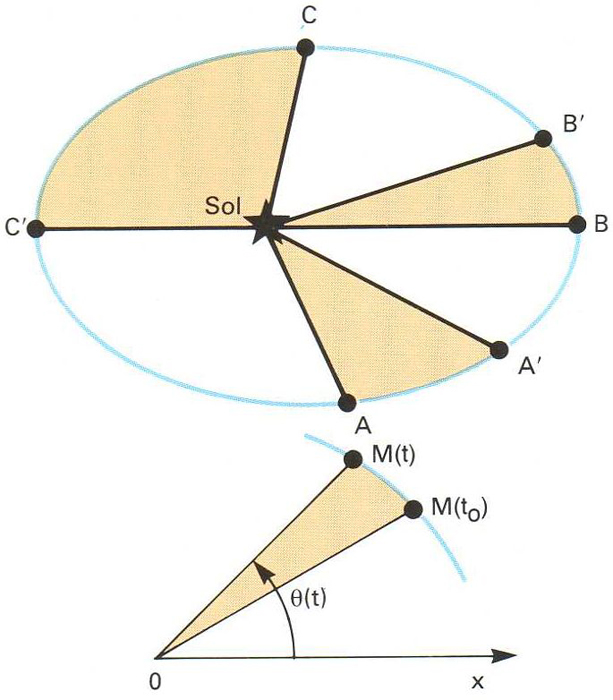
Llei de les àrees aplicada a l’òrbita d’un planeta: les àrees contingudes entre els punts AA’, BB’ i CC’ són iguals perquè es recorren en temps iguals. El radi vector escombra àrees iguals en temps iguals
© fototeca.cat
Física
Teorema referit al moviment d’un punt sotmès a un sistema de forces centrals, que demostra que les àrees descrites pels radis vectors r
©són proporcionals al temps emprat per a descriure-les.
En astronomia, aquest teorema és aplicat a l’estudi del moviment d’un planeta respecte al Sol i és conegut com la segona de les tres lleis de Kepler La demostració és obtinguda d’aplicar el teorema del moment angular al cas particular del moviment d’un punt material M sotmès a un sistema de forces centrals que passen pel punt O , respecte al qual hom obté els moments Aquests moments tenen una resultant nulla i, per tant, el moment angular L és un vector constant perpendicular sempre als radis vectors, que descriuran com a conseqüència una trajectòria plana Si hom considera la posició de M en…
principi de Hamilton
Física
Una de les formes d’enunciar el principi de la mínima acció.
L' acció elemental és definida a partir del lagrangià, dA = L dt , i el principi afirma que el moviment del sistema entre dos instants t 1 i t 2 és tal que l’acció és un extremal, és a dir, un màxim o un mínim Hom en dedueix les equacions de Lagrange
moviment brownià
Física
Agitació contínua de partícules de dimensions microscòpiques (~1μm) en suspensió dins d’un fluid (líquid o gas), causada pels impactes desordenats amb les molècules del medi, les quals es desplacen contínuament per agitació tèrmica.
El nom prové de Robert Brown, que n'observà l’existència el 1827 El valor mitjà dels quadrats de les projeccions x dels desplaçaments d’una partícula qualsevol en una direcció determinada i en temps iguals, és donat per l’expressió següent, deduïda el 1905 per Einstein i M Smoluchowski =2 Dt , essent D=kT/6 πη a el coeficient de difusió k és la constant de Boltzmann, T és la temperatura, η la viscositat del medi i a el radi de la partícula i t el temps Com més petites són les partícules, tant més observable és llur moviment
moment lineal
Física
Donat un cos de massa m que es mou amb una velocitat v, vector p definit per la fórmula p = m v
.
El moment lineal és anomenat també quantitat de moviment , i és, en física, una magnitud fonamental Així, d’una banda, la segona llei de Newton pot éser formulada en termes del moment lineal mitjançant l’anomenat teorema del moment lineal , segons el qual la derivada temporal del moment lineal d’un cos és igual a la força que actua sobre seu, és a dir, d p /dt = F , o bé mitjançant el teorema de l'impuls, que és la forma integrada del teorema del moment lineal D’altra banda, en el cas d’un sistema de cossos, la llei de conservació del moment lineal del sistema definit com a suma…
pèndol
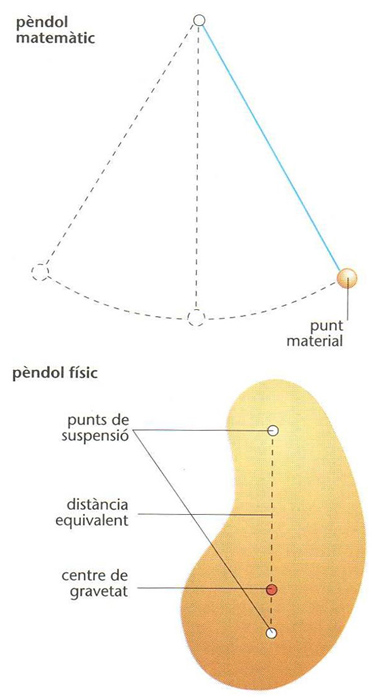
Pèndol
© Fototeca.cat
Física
Sistema físic format per un cos material que oscil·la al voltant d’un eix horitzontal que no passa pel seu centre de gravetat.
Per tal d’establir les lleis del pèndol, hom ha idealitzat l’anomenat pèndol simple o matemàtic , que consisteix en un punt material que penja d’un fil inextensible i sense pes, fixat en un punt immòbil Per a oscillacions de petita amplitud en què sin ϕ ≈ϕ ϕ és l’angle que forma el fil del pèndol en un moment determinat amb la seva posició vertical, el moviment del pèndol satisfà l’equació diferencial d 2 x/dt 2 Y - g/l x , en què x és l’elongació, t el temps, g l’acceleració de la gravetat i l la longitud del pèndol Aquesta equació, que és independent de la massa, no és més que…