Resultats de la cerca
Es mostren 3270 resultats
bisectriu
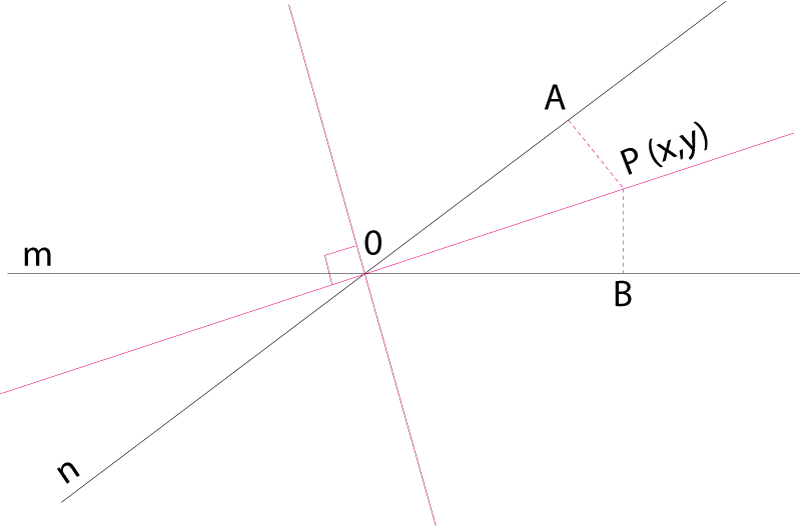
Bisectrius corresponents als quatre angles determinats per dues rectes que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels costats d’un angle, el qual divideix, per tant, en dos angles iguals.
Dues rectes que es tallen determinen quatre angles, iguals dos a dos Llurs bisectrius són dues rectes perpendiculars entre elles En considerar un dels quatre angles hom distingeix la bisectriu interior i la bisectriu exterior Les equacions de les bisectrius dels angles que determinen dues rectes que es tallen, les d’equacions de les quals són, en una referència cartesiana normal, A 1 x + B 1 y + C 1 = 0 i A 2 x + B 2 y + C 2 =0, són
bisector
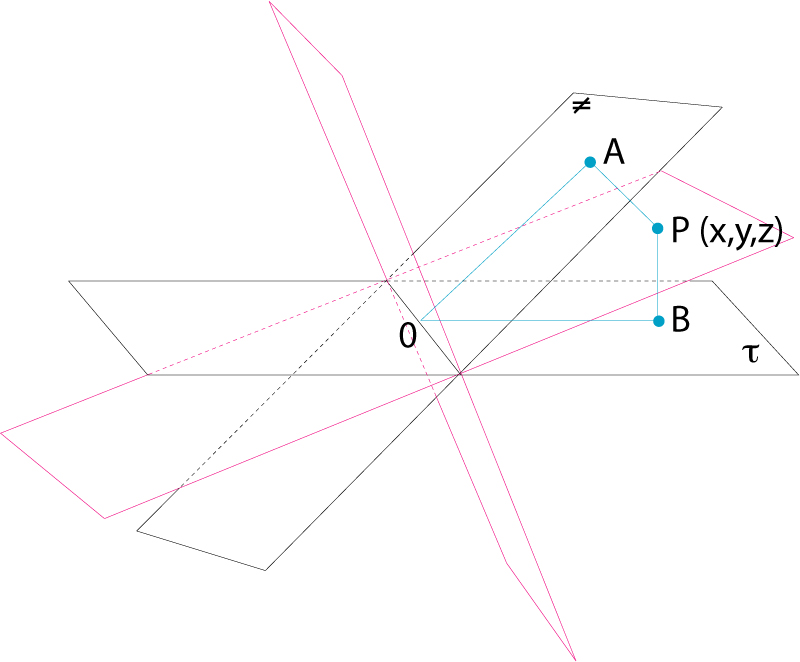
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
sistema binari
Matemàtiques
Electrònica i informàtica
Sistema de numeració de base dos.
En aquest sistema hom només necessita dos signes que representin els nombres zero i u Qualsevol nombre natural pot ésser descompost en suma de potències de 2, i el nombre resta determinat dient quines potències entren en la descomposició indicades amb el coeficient 0 o 1 Així, el nombre 45 = 2 5 + 2 3 + 2 2 + 2 0 és escrit, en sistema binari , 101101 dos Per a passar un nombre donat en el sistema binari al sistema decimal cal tenir en compte que cada unitat en val dues de l’ordre immediat inferior Així, el nombre 1010111 dos és Hom pot també representar, en el sistema binari, els nombres…
relació binària
Matemàtiques
Condició relativa a dos elements d’un conjunt que és satisfeta per determinats parells d’elements (eventualment per tots o per cap parell).
Sovint hom representa una relació binària per una taula de doble entrada on són assenyalats els quadres corresponents als parells que satisfan la relació La taula següent dóna la relació a és múltiple de b entre els nombres del conjunt 1,2,3,4,5,6 Entre les relacions binàries sobresurten per llur importància les relacions d’equivalència i les relacions d’ordre
bifurcació
Matemàtiques
En el context de les equacions no lineals, situació en què, per a algun valor crític d’un paràmetre λ que hi figura, canvia el nombre o l’estructura de les solucions.
Aquest valor crític de λrep el nom de punt de bifurcació La teoria de la bifurcació estudia l’estructura de les solucions de f υ,λ=0 com a funció del paràmetre λ, on f és una aplicació no lineal definida quan υ pertany a V V és un subconjunt d’un espai funcional Els fenòmens de bifurcació tenen un paper important en casos de vinclament de barres o plaques minses, canvi de règim en el moviment dels fluids, cinètica de les reaccions químiques i, en general, en tots els aspectes de la natura en la descripció matemàtica dels quals intervé de manera rellevant la grandària de certs paràmetres
relació d’ordre
Matemàtiques
Relació binària R entre els elements d’un conjunt C que és reflexiva, antisimètrica i transitiva.
La parella C, R constitueix un conjunt ordenat És usual la notació ≤per a designar la relació d’ordre desigualtat 5, i a ≤ b és llegit '' a menor o igual a b' , o bé '' a inferior a b' aquesta notació generalitza la coneguda i usual relació “ésser menor que o igual a” que ordena els nombres Unes altres relacions d’ordre importants són la relació d’igualtat, la relació d’inclusió entre conjunts, la relació “ésser divisor de” en els nombres naturals, etc En un conjunt ordenat, són elements notables el màxim , el mínim , el maximal , el minimal , el majorant i el minorant Dos elements…
ordre d’infinitud
Matemàtiques
Resultat de comparar dues funcions, f(x) i g(x), que prenen el valor infinit quan x s’acosta a un cert valor a
.
Hom diu que f x i g x són del mateix ordre d’infinitud si el límit del quocient f x / g x , quan x tendeix a a , existeix i és una constant no nulla En el cas que el dit límit sigui zero o bé infinit, hom diu, respectivament, que f x és de menor ordre d’infinitud que g x o bé que f x és de major ordre d’infinitud que g x