Resultats de la cerca
Es mostren 3270 resultats
desigualtat
Matemàtiques
Donada una relació d'ordre en un conjunt C, expressió que indica la relació entre dos elements determinats.
L’expressió a < b és una desigualtat entre a i b , i es llegeix ''a és inferior a b' o '' a és anterior a b ' l’expressió a > b es llegeix ''a és superior a b' o '' a és posterior a b ' Amb l’expressió a ≥b hom indica que ''a és inferior o igual a b’ i amb a ≤b que '' a és posterior o igual a b' Quan C és un conjunt numèric, les expressions a b, a ≤b i a ≥b indiquen, respectivament, que a és menor, major, menor o igual o major o igual, que b
desigualtat
Matemàtiques
Expressió mitjançant la qual hom indica la manca d’igualtat que hi ha entre dues quantitats o expressions.
desenvolupament en sèrie
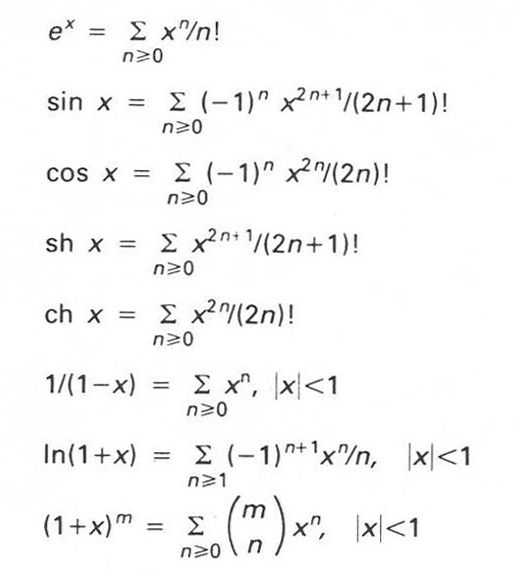
Desenvolupament en sèrie de potències d’algunes funcions
©
Matemàtiques
Expressió d’una funció real, de variable real o complexa,
f(x) ∞
, en termes d’una sèrie de funcions
:
.
La legitimitat d’aquesta igualtat depèn de la convergència de la successió de sumes parcials, en el domini de definició de fx Hom empra, generalment, el desenvolupament en sèrie de potències o sèrie entera, que resulta del teorema de Taylor , i, en el cas de funcions periòdiques, hom empra el desenvolupament en sèrie de Fourier anàlisi de Fourier
desenvolupament
Matemàtiques
Operació consistent a desplegar sobre un mateix pla els elements successius d’una superfície desenvolupable
.
superfície desenvolupable
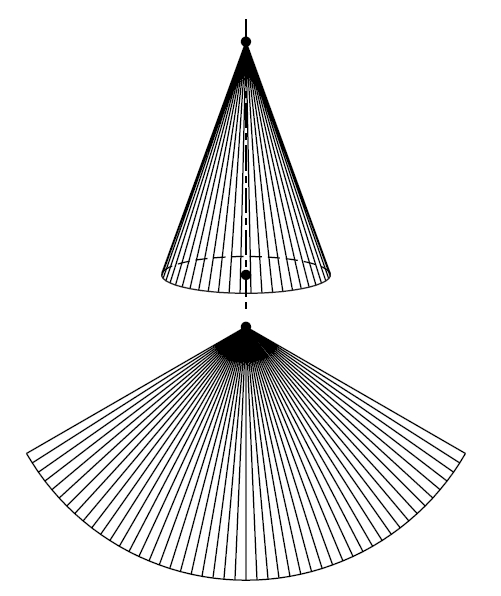
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
descomposició en factors primers a ℤ
Matemàtiques
.
Propietat del conjunt dels nombres enters ℤ, segons la qual tot enter no nul pot expressar-se d’una manera única en la forma b=sp 1 a 1 p n a n , on s=1 o -1, els p i són nombres primers diferents, i els a i són nombres naturals no nuls
derivada parcial d’una funció en un punt
Matemàtiques
Donada una funció real, f:D⊂ℝn→ℝ, i un punt del seu domini de definició, a=(a1,...,an) ∈D, derivada en el punt ai de les funcions d’una variable fi(xi) = f(a1,...,xi,...,an)
.
La i-èsima derivada parcial de f en el punt a és, doncs, el nombre ∂ f/∂x i a = df i /dx i a i Si aquesta és, al seu torn, derivable, hom pot definir derivades parcials d’ordres superiors , com, per exemple, ∂ 2 f /∂ x i ∂x j = ∂∂ f / ∂x i / ∂ x j
derivada logarítmica d’una funció en un punt
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt a∈D, derivada de la funció ln|f(x)| en el punt a
.
Així, doncs, la derivada logarítmica de f en a és f´ a / f a
derivada d’una funció en un punt
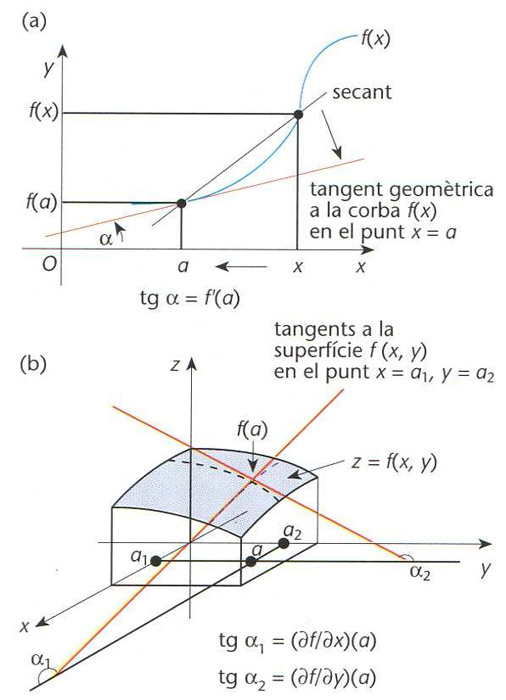
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’ordre…