Resultats de la cerca
Es mostren 3270 resultats
Pierre-Ossian Bonnet
Matemàtiques
Matemàtic francès.
Fou catedràtic d’astronomia matemàtica a la Sorbona des del 1878, i membre de l’Académie des Sciences 1862 Féu treballs d’investigació en els camps de la mecànica, del càlcul infinitesimal, i, especialment, en geometria pura sobre la teoria de superfícies És autor de les memòries La théorie générale des surfaces 1845 i Mémoire sur l’emploi d’un nouveau système de coordonnées dans l’étude des propriétés des surfaces courbes , publicades al “Journal des Mathématiques”
Josep Bonet i Vinyals
Matemàtiques
Matemàtic, germà de Joaquim Bonet i Vinyals.
Professor 1851 i director 1861 de l’Escola de Nàutica de Barcelona Publicà, en collaboració amb Ezequiel Calvet, les famoses Tablas de Logaritmos Españoles 1847 i una Colección de Tablas para varios usos Del 1852 al 1866 publicà amb Joan Dey unes Tablas de declinaciones del Sol y ecuaciones del tiempo
integral múltiple
Matemàtiques
Integral definida sobre un domini D de ℝn.
Donat un domini D de ℝ n , i una partició en dominis elementals D i d’àrees a i i diàmetres d i , i donada una funció real definida sobre D , fD ⊂ ℝ n → ℝ, límit I quan els d i tendeixen a 0, de les sumes de Riemann on A i ∈ D i Hom diu que I és la integral de f en D i és notada per ʃ ʃ n ʃ D ʃ x 1 , x n d x 1 dx n Els casos particulars n =2 i n =3 constitueixen la integral doble i la integral triple, respectivament Les integrals múltiples poden ésser calculades per integració unidimensional reiterada
Tomàs Cerdà
Filosofia
Matemàtiques
Matemàtic i filòsof.
Entrà a la Companyia de Jesús el 1732 Ensenyà filosofia al collegi de Saragossa i a la Universitat de Cervera, i teologia a Girona El seu pensament entra de ple en l’escola eclesiàstica europea del seu temps tan característica de la illustració cristiana, tendent a renovellar l’antiga filosofia amb la ciència moderna Ensenyà matemàtiques al Collegi de Cordelles de Barcelona i al Colegio Imperial de Madrid, on fou també cosmògraf del Consejo de las Indias Amb l’expulsió dels jesuïtes 1767 passà a Itàlia Com a filòsof, en resten les Iesuiticae philosophiae theses Cervera 1753 com a matemàtic,…
jacobià (d’una funció)
Matemàtiques
Determinant de la jacobiana d’una funció, quan aquesta matriu és quadrada, és a dir, quan m = n.
Hom empra la notació J = D f 1 ,, f n / D x 1 ,, x n Rep el seu nom del matemàtic Karl Jacobi
mètode dels mínims quadrats
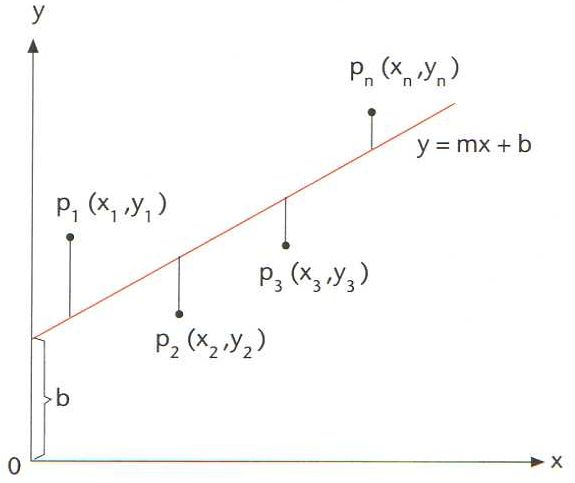
Representació de la recta y=mx + b obtinguda pel mètode dels mínims quadrats
© Fototeca.cat
Matemàtiques
Donat un conjunt de n punts del pla (x1, y1), (x2, y2), ... (xn, yn), mètode que permet de trobar l’equació y = mx + b de la recta que compleix la condició d’ésser la que més s’apropa als punts donats.
Hom defineix matemàticament la dita condició exigint que la suma dels quadrats de les desviacions, ha d’ésser mínima, entenent per desviació en un punt x i , y i la diferència d i = y i - mx i + b Hom pot demostrar que aquella condició condueix a les dues equacions a partir de les quals hom pot calcular els coeficients m i b de la recta, la qual és anomenada també recta de regressió D’altra banda, el mètode dels mínims quadrats serveix també per a ajustar funcions més complexes que la d’una recta, tals com funcions polinòmiques, exponencials, etc, i és utilitzat en l’estudi de la…
funció esglaonada
Matemàtiques
Funció f: [a, b] ⊂ℝ → Osb; tal que existeix una subdivisió del seu interval de definició, a=a0 < a1 < ... < an = b, tal que les restriccions de f a cada interval obert (ai - 1, ai) és una funció constant.
Els punts a i són discontinuïtats de primera espècie
funció polinòmica
Matemàtiques
Donat un polinomi a0 + a1 X + ... + anXn , funció f(x) que fa l’assignació x → a0 + a1x + ... + anxn.
El grau n del polinomi és el grau de la funció polinòmica Quan n = 2 la funció és quadràtica i quan n = 3 és cúbica
independència funcional
Matemàtiques
Propietat de què gaudeix una família de funcions f1, f2, ..., fn quan no existeix cap funció F tal, que F(f1, f2, ..., fn) = 0, on (F (f1, f2, ..., fn) (x) = F(f1 (x), f2 (x), ..., fn(x).
Vegeu també jacobià
Antoni Torroja i Miret
Matemàtiques
Matemàtic.
A Madrid, on residia el seu pare, Eduard Torroja i Caballé, cursà els estudis de matemàtiques i d’enginyer de mines El 1917 guanyà una càtedra de geometria a la Universitat de Saragossa, i al cap de poc passà a la de Barcelona El seu magisteri exercí una gran influència en la formació de noves promocions de matemàtics, especialment per l’educació del raonament que inculcava també tingué una gran influència en els seus cursos de mecànica de l’Escola Industrial La seva producció científica consta d’alguns treballs i comunicacions a congressos sobre la geometria projectiva Fou acadèmic de les…