Resultats de la cerca
Es mostren 46 resultats
àrea
Matemàtiques
Mesura o grandor de l’extensió o porció del pla ocupada per una figura.
La teoria elemental de les àrees dels polígons pren com a unitat d’àrea el quadrat que té per costat la unitat de longitud Un rectangle de costats de longitud entera conté tants quadrats unitat com indica el producte de les seves dimensions Si les mesures dels costats del rectangle són fraccionàries hon divideix els costats en parts iguals, tantes com indiquen els denominadors d’aquelles mesures Resulta sempre la mateixa regla hom obté l’àrea d’un rectangle multiplicant les seves dues dimensions Si les mesures dels costats són irracionals hom pren aproximacions per…
àrea lateral
Matemàtiques
En certs cossos, suma de les àrees de totes les seves parts prescindint de les que són base o tapa.
Així, l’àrea lateral d’un cilindre és l’àrea total menys les àrees dels dos cercles de les dues bases
integral
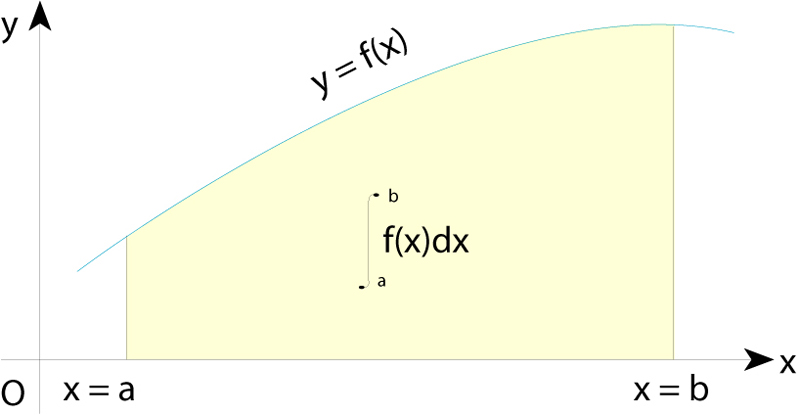
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…
element de superfície
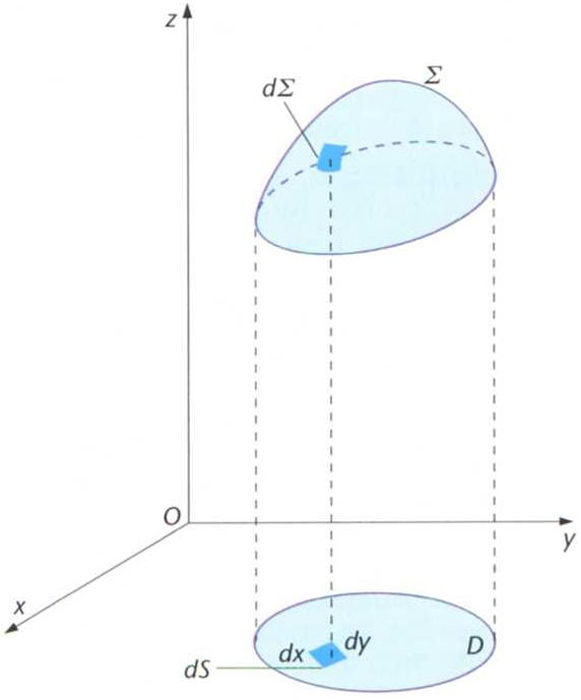
Element de superfície
© fototeca.cat
Matemàtiques
Cadascuna de les parts infinitesimals en què hom divideix una superfície a l’hora de calcular-ne l’àrea.
En coordenades cartesianes l’element de superfície dS val dS = dx dy , i en coordenades polars dS = ρ d ρ d θ L’àrea A d’una superfície regular z = f x,y que tingui com a projecció en el pla XOY un recinte S , és igual a la integral doble expressada per
regla de Simpson
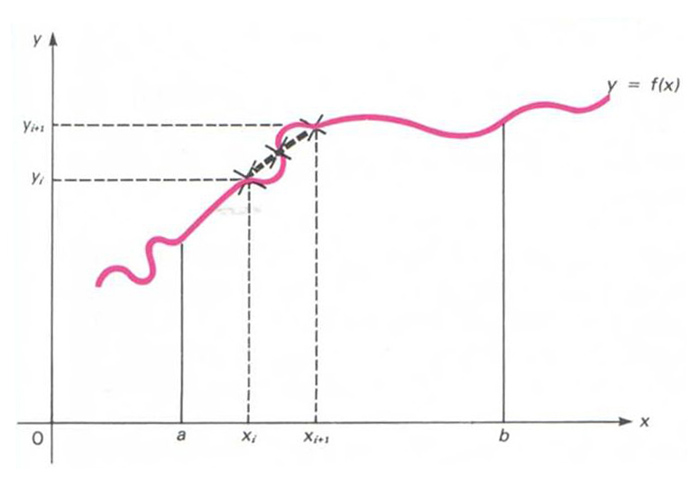
Regla de Simpson
© fototeca.cat
Matemàtiques
Mètode per a aproximar l’àrea limitada per una corba y = f(x), l’eix OX i dues rectes paral·leles x = a i x = b.
El mètode suposa que els petits arcs de la corba són aproximables mitjançant arcs de paràbola que passen pel punt mitjà i pels punts terminals de l’arc considerat La fórmula que hom obté amb aquesta aproximació és usant les sèries de Taylor fins als termes quadràtics on l’interval a,b ha estat dividit en 2 n subintervals a, x 1 , x 2 , , x 2 n - 1 , b , i y a , y 1 , y 2 , , y 2 n - 1 , y b són les respectives ordenades d’aquests punts, y i = f x i La diferència numèrica entre l’àrea real i aquesta àrea aproximativa A , és fitada per la quantitat M b-a 5 /…
inequació isoperimètrica
Matemàtiques
Inequació segons la qual l’àrea a d’una regió plana, limitada per una corba tancada de perímetre L, satisfà a ≤ L2/4π.
Aquesta inequació expressa que entre totes les corbes isoperimètriques del pla, la circumferència és la que conté l’àrea més gran
fórmula del trapezi
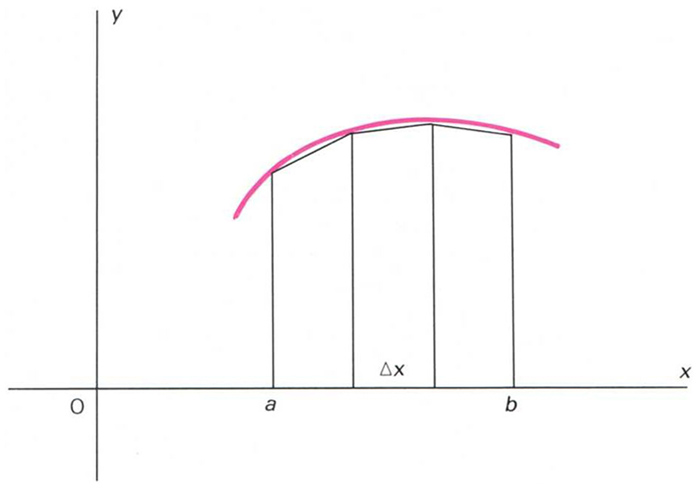
Aplicació de la fòrmula del trapezi
© fototeca.cat
Matemàtiques
Regla utilitzada per a aproximar l’àrea compresa entre una corba, una línia horitzontal i dues de verticals que tallen la corba.
Hom divideix el segment horitzontal en diverses parts iguals i dibuixa les perpendiculars des de cada punt de divisió a la corba després les interseccions d’aquestes rectes amb la corba són unides mitjançant línies rectes, successivament La suma de les àrees dels trapezis així engendrats representa una aproximació de l’àrea limitada per la corba
teoremes de Guldin
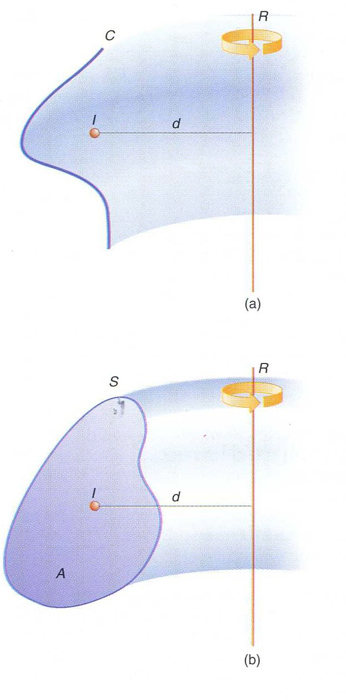
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…