Resultats de la cerca
Es mostren 148 resultats
e
Matemàtiques
Nombre irracional i transcendent definit per
.
Els primers coeficients de la seva expressió decimal illimitada són e= 2,7182818284590 És el límit de la sèrie i és relacionat amb els altres nombres fonamentals de la matemàtica per l’expressió e iπ +1 = 0 La funció de ℝen ℝdefinida per x → e x és la funció exponencial,i la definida per és la funció logarítmica , que assigna a cada nombre real el seu logaritme natural o neperià El nombre e i les funcions associades són de gran interès i utilitat en física i matemàtiques
Carlos Ibáñez e Ibáñez de Ibero

Carlos Ibáñez e Ibáñez de Ibero
© Fototeca.cat
Història
Militar
Matemàtiques
Matemàtic i militar.
El 1839 ingressà a l’acadèmia d’enginyers de l’exèrcit Publicà, amb Joan Modet, un Manual del pontonero 1853 Aquell mateix any fou membre de la comissió que havia de fer el mapa de l’Estat espanyol i inicià, així, els seus notables treballs geodèsics Feu construir, sota la seva direcció, a París, un aparell per a mesurar bases geodèsiques, que fou consultat pel govern egipci fou elegit membre de l’Institut Egipci Fou nomenat cap del primer districte geodèsic cadastral, que comprenia aleshores el País Valencià i les Illes Balears El 1864 publicà Estudio sobre la nivelación geodésica , i el…
Diccionario geográfico, estadístico e histórico de España y sus posesiones de ultramar
Matemàtiques
Obra de Pascual Madoz publicada a Madrid (1845-50) en 16 volums.
Conté moltes dades importants d’Espanya i de les seves característiques geogràfiques, aspectes socials i demogràfics i l’activitat econòmica preponderant Madoz tingué corresponsals arreu que li proporcionaren les dades dels pobles respectius N'han estat fetes diverses edicions facsímils parcials, entre elles la realitzada l’any 1982 per la Institució Alfons el Magnànim de València, que en publicà els articles referents a l’àmbit del País Valencià, i la feta l’any 1985 per Curial Edicions Catalanes, amb els articles referents a l’àmbit de Catalunya
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…
complementari | complementària
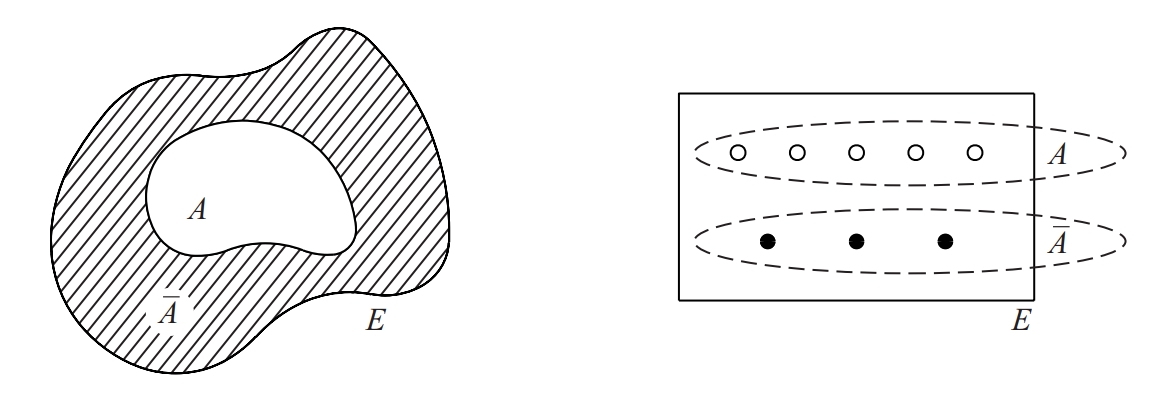
Conjunt complementari (Ā) de A dins E
matroide
Matemàtiques
Estructura algèbrica consistent en un conjunt E i un conjunt S de parts no buides de E que satisfan: tot singletó de E pertany a S
.
Si X ∈S , aleshores tota part Y no buida de E inclosa en X pertany també a S i, per a tota part A de E , si X i Y són dos elements de S continguts en A i maximals, aleshores card X = card Y La teoria de matroides fou introduïda per Withney el 1935 i ha experimentat un desenvolupament ràpid en ésser aplicada als espais vectorials i a la teoria de grafs
element simètric
Matemàtiques
Element x’ tal, que xTx’ = x’Tx = e
.
Si aquesta propietat existeix, hom diu que x’ és l’element simètric o invers de x, x ∈E , E essent un conjunt dotat d’una llei interna T i d’un element neutre e, i x, simetritzable
base dual
Matemàtiques
Base definida en un espai vectorial E de dimensió finita.
Si e 1 , e n és una base de E , aleshores el conjunt de formes lineals f i E→K, amb imatges sobre el cos K de l’espai vectorial, definits per f i e j =δ i j , essent δ i j =0 si i ≠ j , δ ij =1, forma una base de l’espai dual E *, i s’anomena la base dual de la inicial
funció homogènia
Matemàtiques
Funció f:E→ℝ, on E és un espai vectorial, que satisfà f(λx) per a tot x∈E i λ∈ℝ.
Hom diu, concretament, que f és una funció homogènia de grau α, i α∈ℝés el grau d’homogeneïtat de f En el cas que E =ℝ n una funció homogènia de grau α satisfà f λ x 1 ,, x n =λ α -
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina