Resultats de la cerca
Es mostren 6 resultats
variable aleatòria de Bernoulli
Matemàtiques
Variable aleatòria x susceptible de prendre dos únics valors, 0 i 1, amb probabilitats p i q = 1-p, respectivament.
valuació
Matemàtiques
Funció que fa correspondre a cada proposició el seu valor de veritat, si aquest existeix.
En el cas de la lògica binària clàssica els únics valors de veritat que s’admeten són veritat 1 i fals 0, però en les lògiques polivalents hom accepta un tercer valor 1/2 que admet interpretacions diverses per exemple, possible o indeterminat La taula de veritat bivaluada o polivalent de dues proposicions reflecteix totes les possibles valuacions o assignacions de valors de veritat
mosaic
mosaics
© Fototeca.cat
Matemàtiques
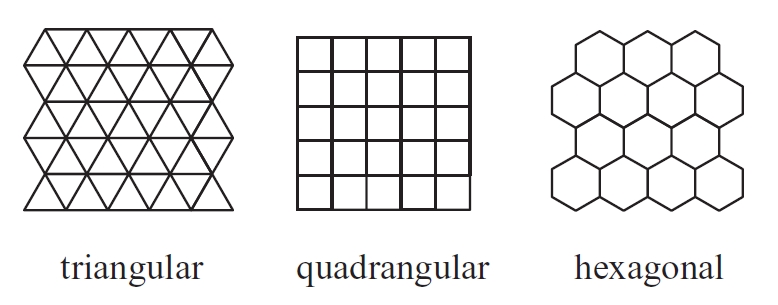
Recobriment del pla per repetició d’un mòdul fix segons dues direccions.
Els mosaics regulars s’obtenen per repetició d’un polígon regular Els mosaics semiregulars es generen en combinar dos tipus de polígons regulars de dimensions convenients per al seu acoblament Únicament hi ha tres tipus de mosaics regulars i vuit de semiregulars Els únics mosaics regulars que es poden construir al pla són el triangular, el quadrangular i l’hexagonal
obert | oberta
Matemàtiques
En un espai mètric E, dit del conjunt C tal, que donat un punt qualsevol a de C existeix una distància d tal, que tots els punts de E situats a una distància del punt a inferior a d pertanyen al conjunt C.
Així, entre els intervals de la recta real, els únics oberts són els intervals oberts interval Les propietats formals dels conjunts oberts han conduït a la formulació de l’anomenada topologia general , en la qual la noció d’obert és una noció primitiva que només és subjecta als tres axiomes següents el conjunt buit és obert, tota unió de conjunts oberts és un conjunt obert, i tota intersecció finita de conjunts oberts és un conjunt obert
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…