Resultats de la cerca
Es mostren 6 resultats
Marc Aurel
Matemàtiques
Matemàtic.
Mestre d’escola, d’origen alemany i radicat a València És autor de Tratado muy útil o provechoso para toda manera de tratantes 1541 i Libro primero de Aritmética algebraica en el qual contiene el arte mercantívol 1552, primer manual d’àlgebra publicat en castellà, inspirat en la Summa de Lucas de Burgo i en Algebre de Christof Rudolf Aquesta obra estimulà els estudis d’aritmètica i sobretot d’àlgebra a la península Ibèrica
nombre enter
Matemàtiques
Nombre que determina quantitats no fraccionables en parts més petites que la unitat.
La manera més simple d’introduir els nombres enters, positius i negatius, és imaginar una escala gràfica en la qual, a partir d’un punt elegit com a origen i designat amb el nombre zero , que no és positiu ni negatiu, hom senyala segments iguals en un sentit i en l’altre, designats amb els nombres naturals successius 1, 2, 3, , als quals hom afegeix, per tal de distingir els sentits, el signe + o el signe - Des d’aquest punt de vista, hom pot dir que un nombre enter és un nombre natural precedit d’un signe +o- Aquesta manera d’introduir els nombres enters, que és molt útil des…
axonometria
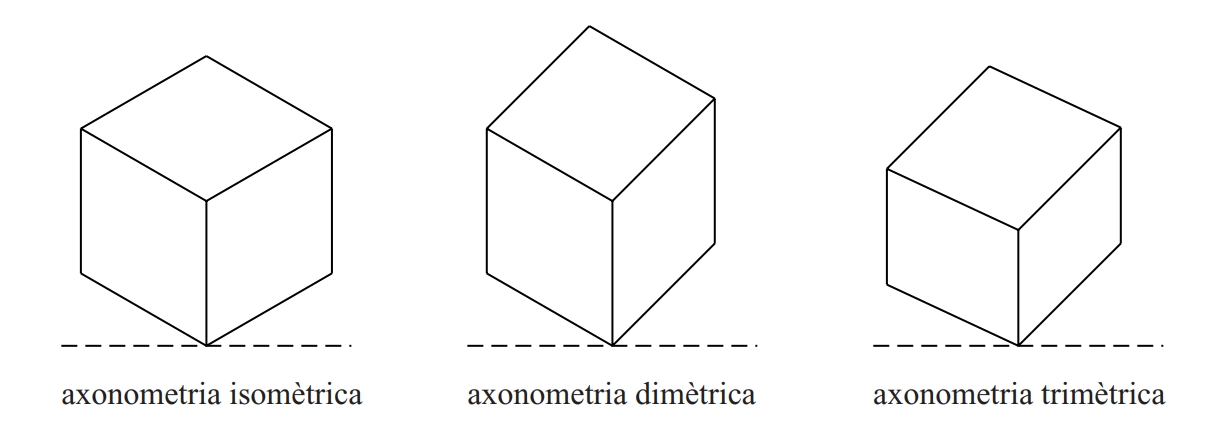
axonometria
© Fototeca.cat
Matemàtiques
Mètode de representació de les figures de l’espai.
En aquest sistema hom pren un tríedre trirectangle com a referència i determina cada punt de l’espai per les seves projeccions ortogonals damunt els plans del tríedre Després hom projecta sobre el pla del dibuix la figura formada pel tríedre, el punt i les seves projeccions sobre els plans del tríedre És útil, per a fixar bé la posició de la figura a l’espai, de dibuixar les interseccions dels plans del tríedre amb el pla de dibuix Aquestes rectes d’intersecció són anomenades traces Projecció axonomètrica d’un cub © Fototecacat Per a determinar les projeccions d’un punt convé de…
teoria de distribucions
Matemàtiques
Part de l’anàlisi matemàtica (i, en particular, de l’anàlisi funcional) que estudia els funcionals lineals continus sobre l’espai vectorial topològic de les funcions reals infinitament diferenciables de suport compacte de ℝn.
L’origen de la teoria té lloc en el càlcul simbòlic de Heaviside del final del segle XIX, el qual fou emprat sistemàticament pels físics i pels enginyers en la resolució de problemes teòrics d’electricitat Posteriorment, l’any 1926, Dirac introduí la seva funció d delta de Dirac com a instrument de treball que ajuda en el tractament de problemes de mecànica quàntica Paradoxalment, tant en el càlcul simbòlic com en els treballs de Dirac, malgrat que hom cometia una sèrie d’abusos de llenguatge i d’incorreccions matemàtiques, els resultats pràctics eren bons No fou fins després del 1945 que…
sistema de coordenades
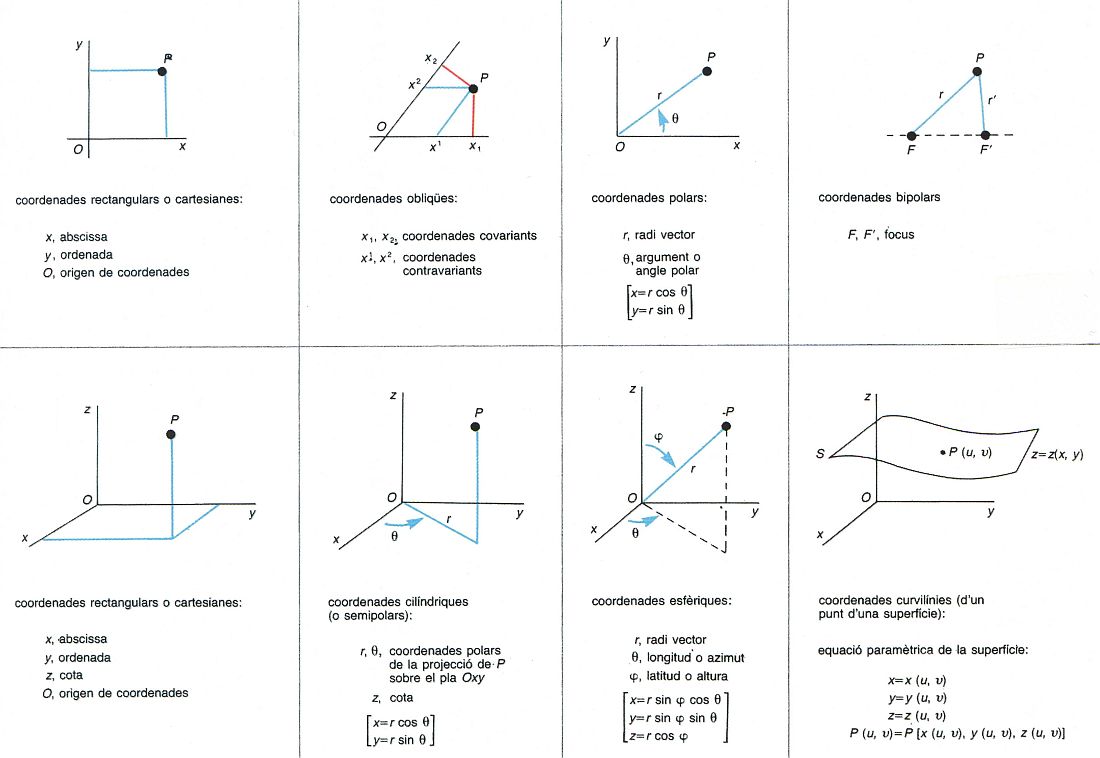
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…