Resultats de la cerca
Es mostren 9 resultats
funció logarítmica complexa
Matemàtiques
Funció f:ℂ-{0}→ℂque resulta d’estendre a ℂla funció exponencial.
És definida per l’assignació z →ln z =ln| z |+ i arg z , on | z | és el mòdul de z i arg z el seu argument És la funció inversa de la funció exponencial complexa e l n z =ln e z = z
funció zeta
Matemàtiques
Funció complexa, introduïda per Riemann.
Definida per la fórmula on z = x + iy ∈ℂés tal, que x > 1 i ln n és real És una funció meromorfa amb un pol simple en z = 1
mòdul dels logaritmes decimals
Matemàtiques
Logaritme decimal del nombre e:M=log1 0 e=0,434 294 481 9....
Permet de relacionar els logaritmes decimals i els neperians mitjançant la fórmula del canvi de base del logaritme L’invers d’aquest mòdul és el logaritme neperià de 10 1/ M =ln 10= 2,302 585 093
nombre de Gould
Matemàtiques
Nombre donat per l’expressió [[ln(640×3203+744)]/π]2.
És un nombre enter mitjançant un nombre transcendent és igual a 163 seguit de trenta zeros decimals, un dos, etc
funció exponencial
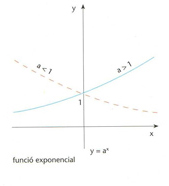
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la…
logaritme
Matemàtiques
Donat un nombre b, real, positiu i distint d’1 (anomenat base), i un nombre qualsevol n real i positiu, nombre a tal, que b, elevat a a, és igual a n, o sia, ba= n.
Hom l’anomena logaritme de base b de n , i el representa per log b n = a Les propietats fonamentals dels logaritmes són Els logaritmes constitueixen un instrument matemàtic que facilita i abreuja molts càlculs complicats Els més utilitzats correntment en el càlcul són els logaritmes decimals, vulgars o de Briggs , que són els logaritmes de base 10 i que hom representa amb els símbols log 1 0 , log o lg Per contra, en els càlculs diferencial i integral són utilitzats els logaritmes naturals o neperians , que són els logaritmes de base e , i hom els representa amb els símbols log e , ln…
constant d’Euler
Matemàtiques
Límit quan n →∞; de la sèrie {un}, n>0, de terme general un= 1+1/2+1/3+...+ 1/n-ln n.
El seu valor aproximat és C = 0,577 215 66
derivada logarítmica d’una funció en un punt
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt a∈D, derivada de la funció ln|f(x)| en el punt a
.
Així, doncs, la derivada logarítmica de f en a és f´ a / f a