Resultats de la cerca
Es mostren 14 resultats
centroide
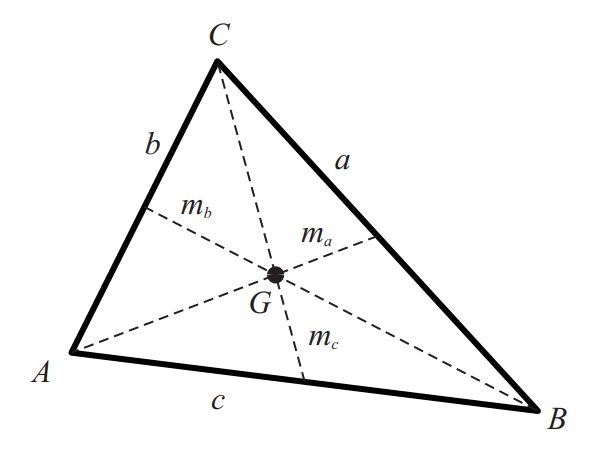
del triangle ABC
Física
Matemàtiques
Punt especial associat a una figura o a una distribució de punts que en el cas físic correspon al centre de massa o de gravetat, de vegades anomenat també baricentre.
En algunes figures el seu centroide és determinat geomètricament Per exemple, en un triangle és el punt d’intersecció de les mitjanes, i en els polígons políedres regulars és el centre de la circumferència esfera circumscrita Donat un conjunt discret de punts x 1 ,, x n amb masses m 1 ,, m n , punt que té per coordenades la mitjana de les coordenades dels punts ponderada per les masses En altres figures es poden trobar per integració les expressions de les coordenades del centroide Així, en figures amb una distribució de massa contínua φ x , el centroide és el punt x̄ = ƒφ x xdx…
teoremes de Guldin
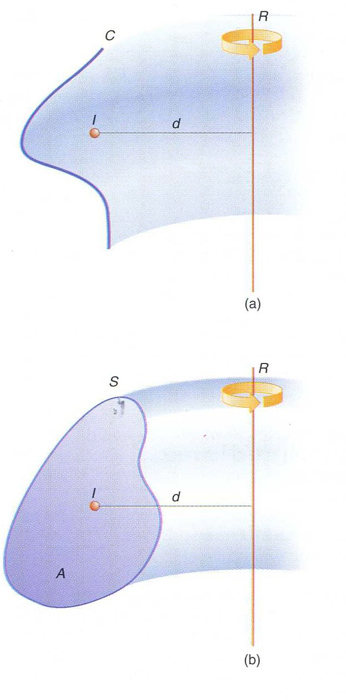
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que,…
Torbern Olof Bergman
Biologia
Matemàtiques
Científic suec conegut pels seus treballs sobre química, bé que els seus estudis inicials foren en el camp de les matemàtiques i de la història natural.
Ocupà la càtedra de química de la Universitat d’Uppsala investigà sobre l’afinitat dels elements fou el primer que assenyalà la influència de la concentració en un sistema de dues sals dissoltes i en equilibri i el mecanisme de desplaçament d’aquest, observacions que molt posteriorment conduïren a la llei d’acció de massa Fou autor de nombrosos treballs sobre mineralogia, geologia i astronomia
condicions inicials
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui, ella i les seves derivades, uns determinats valors per a un valor especificat de la variable independent.
Les condicions inicials permeten, doncs, de determinar la solució particular del problema en ajustar les constants arbitràries de la solució general Per exemple, en el problema del moviment d’una massa puntual, un cop conegudes les forces que hi actuen, el moviment concret que realitza depèn només de la posició i la velocitat en un instant inicial, x t o i v t o , essent aquestes les condicions inicials del problema
Colin Maclaurin
Matemàtiques
Matemàtic escocès.
A la seva obra fonamental, A Treatise of Fluxions 1742, prolongà amb mètodes originals els càlculs del seu mestre INewton sobre determinades qüestions encara no aclarides del tot, com la figura d’equilibri d’una massa fluida en rotació, l’atracció exercida per un ellipsoide homogeni sobre punts de la seva superfície o el seu interior, etc Establí també la fórmula que duu el seu nom, sobre el desenvolupament en sèrie de funcions És autor de Geometria organica 1719, i descobrí un nou mètode de descripció de les còniques
Arthur Stanley Eddington
Astronomia
Filosofia
Matemàtiques
Matemàtic, astrofísic i filòsof britànic.
Estudià a la Universitat de Manchester i en el Trinity College de Cambridge L’any 1906 fou nomenat director assistent del Royal Observatory de Greenwich, i l’any 1913 esdevingué professor d’astronomia i filosofia experimental de la Universitat de Cambridge L’any 1914 fou nomenat director de l’observatori de la universitat, càrrec que mantingué fins a la seva mort De l’any 1921 al 1923 presidí la Royal Astronomical Society Entre els seus estudis més importants es destaquen unes investigacions teòriques sobre el moviment, l’estructura interna i l’evolució dels estels Investigà també teòricament…
atzar
Matemàtiques
Conjunt de causes inconegudes que produeixen un efecte no previsible; un fenomen és atribuïble a l’atzar, o és fortuït o és aleatori, quan no és ni inevitable ni impossible.
Una característica important d’aquests fenòmens és que llur realització depèn d’un conjunt de condicions massa complexes per a poder-les conèixer i estudiar totes Un esdeveniment que apareix inevitablement quan es produeix un conjunt de condicions és un esdeveniment cert respecte a aquestes hom anomena impossibles els que mai no poden aparèixer Els esdeveniments fortuïts són els que tant poden donar-se com no donar-se si es realitzen les condicions és a dir, si aquestes no reflecteixen del tot les condicions necessàries i suficients perquè es realitzi l’esdeveniment, i es tracta…
mesura
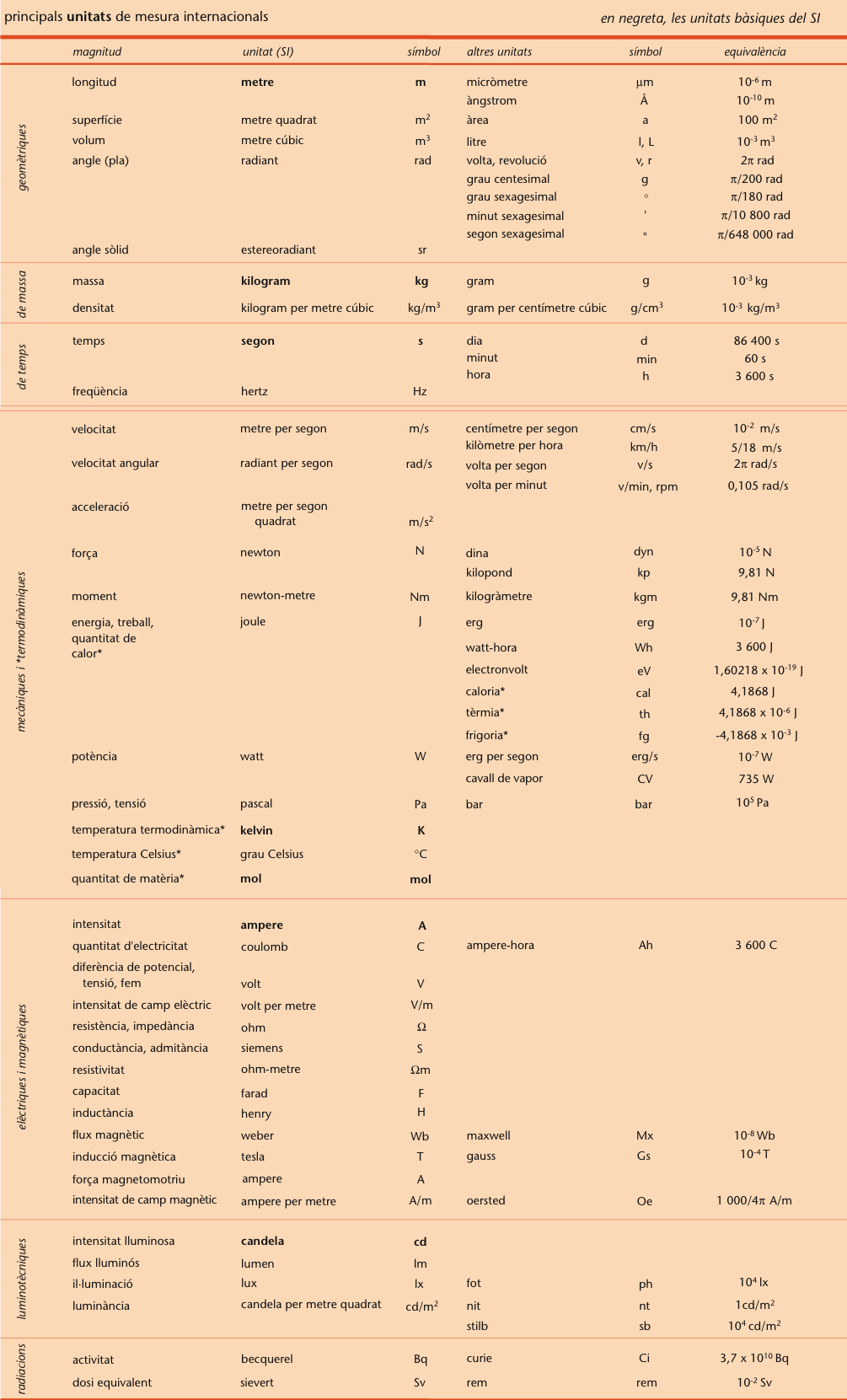
Principals unitats de mesura internacional
© Fototeca.cat
Física
Matemàtiques
Valor numèric obtingut experimentalment com a resultat d’un mesurament consistent a comparar una magnitud amb una altra de la mateixa espècie elegida com a unitat
, amb la finalitat d’establir unes relacions o la deducció d’unes conclusions.
Certes mesures, però, poden ésser de tipus qualitatiu “sí o no”, “més gran que o igual a”, “lineal”, etc, o poden estar relacionades amb una entitat gràfica d’imatge que serà donada per una “concentració” o per una probabilitat obtinguda per repetició del fet experimental El procés de mesura ha d’ésser objectiu i, per tant, la comparació ha d’ésser feta amb una magnitud unitat de la mateixa espècie i de similar dimensió Si hom l’efectua per un procés indirecte transductor, la magnitud final ha d’ésser calibrada en unitats de la magnitud primitiva No totes les magnituds són mesurables en un…
Henry Eyring
Física
Matemàtiques
Químic nord-americà, pioner en l’aplicació de la mecànica quàntica i estadística a la química; establí una teoria sobre les proporcions de reaccions absolutes, i sobre l’activitat òptica, sobre l’espectrometria de massa, bioluminescència i l’addició de dipols i longitud d’enllaços en polímers flexibles.
Publicà, entre altres obres The Kinetic Basis of Molecular Biology 1954, The Theory of Rate Processes in Biology and Medicine 1974 i Deformation Kinetics
Arquimedes
Física
Matemàtiques
Matemàtic i físic grec.
Fill d’un astrònom, hom el suposa parent del tirà de Siracusa, Hieró Fou mort per un soldat romà quan les tropes de Marcel saquejaren Siracusa en el curs de la segona guerra Púnica És difícil de destriar la veritat de la llegenda en els altres detalls de la seva biografia Es destacà en geometria pura Havia estudiat Euclides i tingué alguna relació amb Eratòstenes Hom li pot suposar, però, una certa oposició enfront de la ciència oficial de l’època detinguda pels professors que residien a Alexandria, atesos la profunda originalitat de la seva obra científica, el dialecte dòric en…