Resultats de la cerca
Es mostren 244 resultats
logaritme augmentat
Matemàtiques
Logaritme decimal d’un nombre menor que 1, a la característica del qual, que és negativa, hom ha aplicat cert artifici per tal que sigui sempre positiva.
L’artifici consisteix a sumar a la característica el nombre de desenes positives que calgui per tal que sigui positiva, tot posant aquest nombre de desenes com a superíndex de la característica superíndex que hom anomena augment Així, hom substitueix la característica negativa a per 10 n - a n , n essent un nombre enter positiu tal que 10 n > ¦ a ¦ Els logaritmes augmentats foren ideats per tal de disminuir les probabilitats d’error en les operacions amb logaritmes en certs tipus de càlculs, com en els de navegació astronòmica, artilleria,…
funció monòtona a trossos
Matemàtiques
Funció f: [a,b]⊂ℝ→tal que existeix una subdivisió del seu interval de definició, a = a0 <a1 <... <an = b, tal que, per a tot i=1,...
< a n = b , tal que, per a tot i =1,, n , existeix una funció f i monòtona en l’interval tancat a i - 1 , a i i igual a en l’interval obert a i - 1 , a i
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per exemple, la categoria dels grups G r és…
subcòs
Matemàtiques
Qualsevol subconjunt L d’un cos K tal, que és estable per les dues operacions de K i, mitjançant aquestes restriccions, L té també una estructura de cos.
L és subcòs del cos K si L és un subanell unitari tal, que l’invers de tot element no nul de L pertany a L El conjunt de nombres racionals és un subcòs del conjunt de nombres reals el qual té estructura de cos
gràfic de control
Matemàtiques
Representació cronològica d’observacions relatives a mostres tretes d’un procés industrial per tal de controlar les característiques del producte i corregir, si cal, el funcionament del procés.
En el gràfic de control hom representa, generalment, les mitjanes i les amplituds diferència entre el valor més gran i el més petit de la mostra de les mostres El sistema de referència és constituït per uns eixos de coordenades i unes rectes horitzontals o límits que indiquen la necessitat d’extreure una mostra complementària límit d’atenció o bé d’intervenir directament en el procés per tal de corregir-lo límit d’intervenció
subgrup
Matemàtiques
Qualsevol subconjunt H d’un grup (G, E) tal, que és estable per a l’operació del grup i té estructura de grup mitjançant aquesta operació induïda.
És un subconjunt no buit tal, que si x, y són d’ell, el resultat x-y també hi pertany El conjunt d’enters amb l’operació addició és un subgrup del grup additiu de nombres racionals Si hom divideix l’ordre de G grup per l’ordre de H, el quocient és anomenat índex de H en G o, simplement, índex de H Segons el teorema de Lagrange, si un grup G té ordre finit i H és qualsevol subgrup de G, l’ordre de G és el producte de l’ordre de H per l’índex de H
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat indueix una topologia prenent com a…
axioma de l’elecció
Matemàtiques
Axioma que admet que, donat un conjunt A, existeix una aplicació f del conjunt dels subconjunts no buits de A en A tal que f(B) pertany a B per a tot B de A diferent del buit.
D’una manera informal, l’aplicació f escull un element de cada subconjunt no buit de A Cal fer notar que no és un axioma constructiu, en el sentit que no es té cap indicació sobre la manera de construir una tal f L’axioma de l’elecció equival a la possibilitat de dotar qualsevol conjunt d’una bona ordenació teorema de la bona ordenació L’axioma de l’elecció és equivalent al lema de Zorn
punt de retrocés
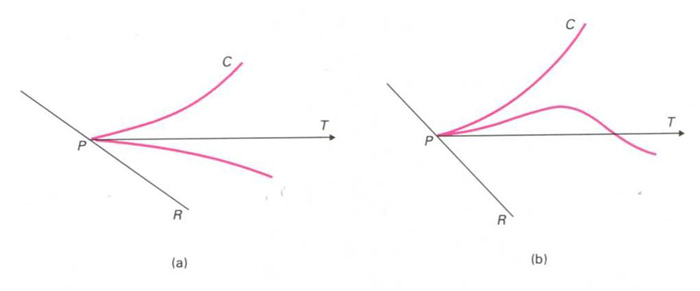
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina