Resultats de la cerca
Es mostren 11 resultats
derivada d’una funció en un punt
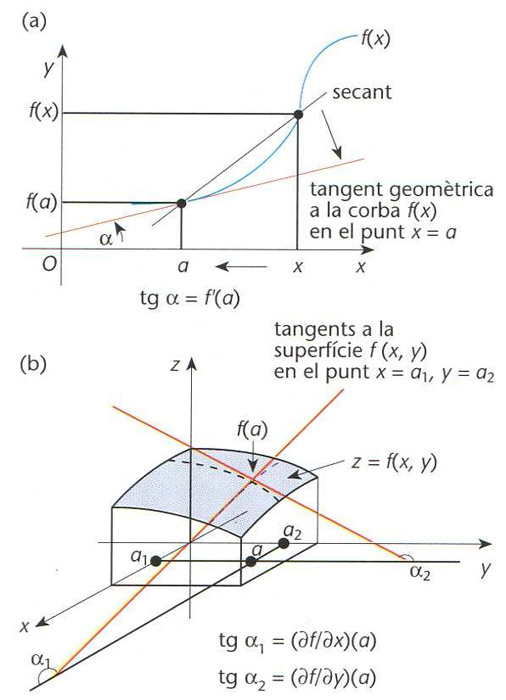
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’ordre…
arc
Matemàtiques
Segment o part d’una corba.
Usualment també designa una corba oberta completa Les característiques d’un arc llargada, corda, fletxa depenen de la corba a la qual pertany En el cas d’una circumferència, hom mesura els arcs en unitats d'angle i un arc val igual que l'angle en el centre que el limita en trigonometria, però, hom considera a vegades que un arc de circumferència α, mesurat en radians, admet una infinitat de determinacions que difereixen per un nombre enter de circumferències i són donades per la fórmula α + 2 k π, on k pot ésser zero o un enter qualsevol El principal problema que es planteja a propòsit d’un…
sinusoide
Matemàtiques
Corba les ordenades de la qual són proporcionals als sinus de les abscisses corresponents.
L’equació general de la sinusoide és f x = A sin Bx , on A i B són constants
subtangent
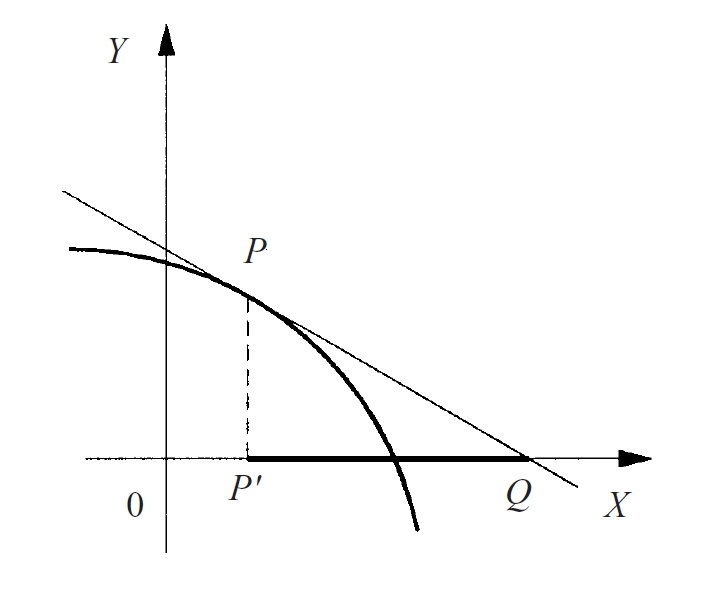
subtangent
Matemàtiques
Segment de la projecció sobre l’eix d’abscisses de la tangent a una corba en un punt, comprès entre la projecció del punt de contacte i la intersecció de la tangent amb l’eix d’abscisses.
angle d’inclinació d’una recta
Matemàtiques
Angle no negatiu que es mesura des de l’eix d’abscisses fins a la recta donada.
La seva mesura és no negativa i inferior a 180°
catenoide
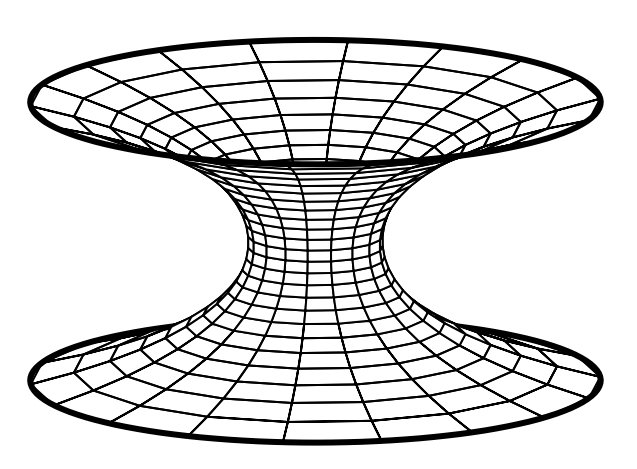
catenoide
Matemàtiques
Superfície mínima de revolució generada per una catenària que gira al voltant de l’eix d’abscisses.
integral
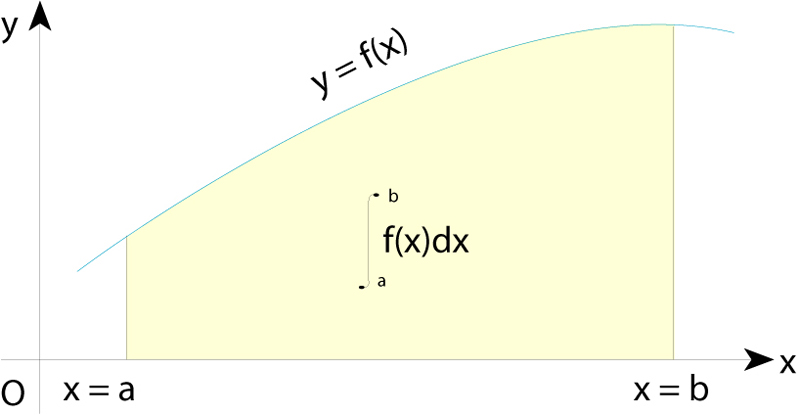
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…
sinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x i y, i un segment de longitud unitat OP que forma un angle α amb l’eix d’abscisses x, valor de la projecció de OP sobre l’eix y
.
Aquesta projecció és el sinus de l’angle α i és denotada per sinα El sinus de l’angle α determinat entre dos segments qualssevol és el sinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al sinus d’un angle són sinα+β = sinα cosβ - cosα sinβ sin-α = -sinα sinα sinβ = cosα-β - cosα+β/2 sinα + sinβ = 2 sinα+β/2 cosα-β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α+sin 2 α=1
angle polar
Matemàtiques
Coordenada que forma part d’un sistema de coordenades polars del pla, i que indica l’angle format per l’eix de les abscisses i la semirecta que determina el punt donat amb l’origen.
L’angle polar és sempre la segona coordenada
cosinus d’un angle
Matemàtiques
Donats dos eixos perpendiculars x
i y
, i un segment de longitud unitat OP
que forma un angle α amb l’eix d’abscisses x
, valor de la projecció de OP
sobre l’eix x
.
Aquesta projecció és el cosinus de l’angle α i és denotada per cos α El cosinus de l’angle α determinat entre dos segments qualsevol és el cosinus de l’angle que, dibuixat sobre aquest cercle goniomètric, té la mateixa obertura que α Algunes fórmules trigonomètriques relatives al cosinus d’un angle són cosα+β=cosα cosβ-sinα sinβ cos-α= cosα cosαcosβ = cosα+β+cosα-β/2 cosα + cosβ = 2 cosα + β/2cosα - β/2 Entre el cosinus i el sinus d’un angle hi ha la relació fonamental cos 2 α + sin 2 α = 1