Resultats de la cerca
Es mostren 28 resultats
intersecció
Matemàtiques
Conjunt format per elements que pertanyen alhora a dos conjunts o més.
La intersecció de dos conjunts, A i B , és denotada per A ∩ B , i es llegeix A intersecció B En geometria, hom parla d’interseccions entre corbes i superfícies
bijectiu | bijectiva
Matemàtiques
Dit de l’aplicació d’un conjunt en un altre que és alhora injectiva i exhaustiva.
relació
Matemàtiques
Lligam entre diversos elements d’un conjunt.
Per tal de precisar aquesta idea intuïtiva, hom defineix la relació com a qualsevol subconjunt d’un producte cartesià del conjunt amb ell mateix és a dir, que els elements són relacionats si formen un element del subconjunt En general, en una relació intervé un nombre determinat d’elements n així, una relació d’ordre entre els elements és un subconjunt del producte de n conjunts A El tipus de relació més freqüent és aquella en què n = 2, anomenada relació binària , que és un subconjunt de A × A Si els dos elements són a i b , hom diu que a R b , o que a és relacionat amb b —o sia, que a,b…
postulat de continuïtat
Matemàtiques
Un dels postulats que establí David Hilbert en els Grundlangen der Geometrie (1899), on precisà l’axiomatització completa i rigorosa de la geometria euclidiana.
Alhora, imposa axiomàticament l’arquimedianitat i la completesa de la recta geomètrica
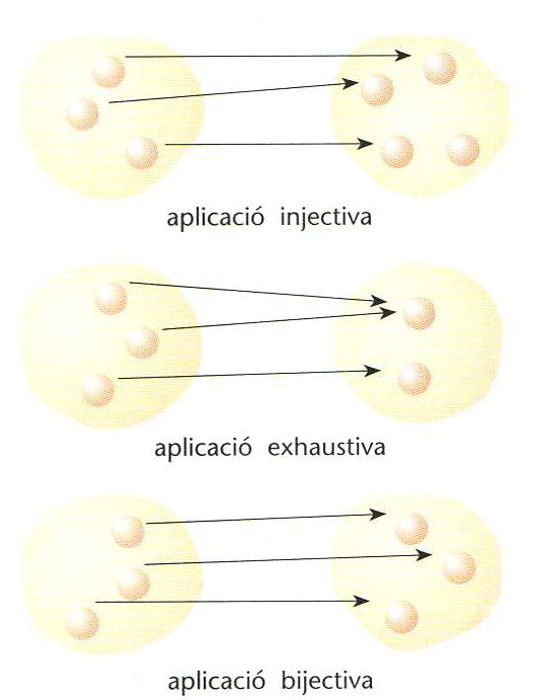
aplicació
fototeca.cat
©
Matemàtiques
correspondència
entre dos conjunts en què tot element del primer conjunt (o original) té una imatge i una de sola en el segon conjunt.
Si elements diferents tenen imatges diferents, l’aplicació és dita injectiva si tot element del segon conjunt és imatge d’un element almenys del primer, l’aplicació és exhaustiva una aplicació que sigui alhora injectiva i exhaustiva és dita bijectiva o unívoca
connex | connexa
Matemàtiques
Dit de l’espai topològic les úniques parts obertes i alhora tancades del qual són el conjunt buit i el propi conjunt.
Alfred James Lotka
Matemàtiques
Demografia
Demògraf i matemàtic nord-americà.
Fou el fundador de la demografia matemàtica i el definidor de les nocions de població estable i estacionària Juntament amb VVolterra, veié la possibilitat d’estudiar alhora la dinàmica de dues poblacions, procedint l’una com a depredador i l’altra com a presa Definí la taxa de creixement natural És autor, entre altres obres, d' Elements of Mathematical Biology 1924 i de Théorie analytique des associations biologiques 1934
paral·lelogram
Matemàtiques
Quadrilàter que té els costats oposats paral·lels i, per tant, iguals.
Les diagonals d’un parallelogram es tallen en llur punt mitjà, anomenat centre del parallelogram Si un parallelogram té els quatre costats iguals, és anomenat rombe Si els quatre costats són perpendiculars, és anomenat rectangle Els parallelograms que són rombes i rectangles alhora són anomenats quadrats , i els que no són ni rombes ni rectangles, romboides L’àrea d’un parallelogram resulta de multiplicar la longitud d’un costat, que hom anomena base , per la distància que el separa del seu parallel, anomenada altura
cub
Matemàtiques
Políedre regular format per sis cares quadrades.
Les tres arestes concurrents a cada vèrtex són perpendiculars entre elles en conseqüència, el tríedre format per les tres arestes és trirectangle, els díedres definits per dues cares amb una aresta comuna són rectes, i les cares oposades són paralleles Les quatre diagonals del cub es tallen en un punt, el centre del cub, que és, alhora, el centre de simetria d’aquesta figura Si la longitud de l’aresta del cub és a , el volum del cub val a 3 , i la seva diagonal té una longitud de a √3
condicions de contorn
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui uns determinats valors en punts o zones concrets del domini de valors de la variable independent, zones anomenades contorns del problema.
Per exemple, el potencial electroestàtic d’una distribució de càrregues elèctriques ha de satisfer l’equació diferencial de Laplace ∇ 2 V =0 amb la condició de contorn que V sigui constant sobre la superfície dels conductors que hi hagi a l’espai del problema Les condicions de contorn són imposades per les lleis físiques, per la simetria o per la disposició experimental del problema Si el problema dinàmic és controlat per una o diverses equacions diferencials en derivades parcials, la solució particular del problema generalment ha de satisfer, a més d’unes condicions de contorn, unes…