Resultats de la cerca
Es mostren 9 resultats
factorial
Matemàtiques
Producte dels nombres naturals consecutius, des de l’1 fins al nombre del qual hom calcula el factorial.
És indicat per n La generalització de la noció de factorial a nombres no naturals és possible mitjançant la funció Γ d’Euler gamma Per a molt gran, hom pot calcular n aproximadament per mitjà de la fórmula de Stirling
superfície de revolució
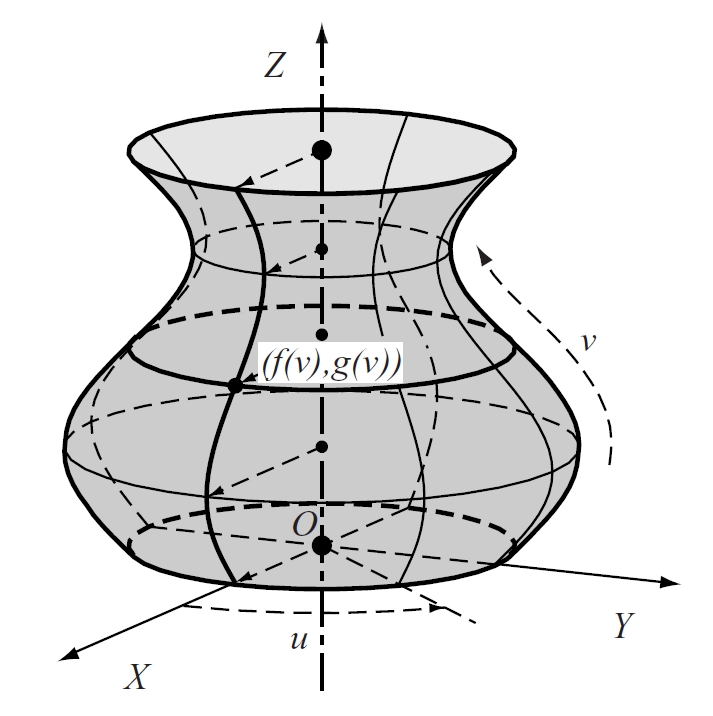
Superfície de revolució
Matemàtiques
Superfície engendrada per la rotació d’una corba (generatriu) entorn d’un eix, anomenat de revolució.
Si aquesta corba és plana i situada en un pla que conté l’eix és anomenada meridiana de la superfície La circumferència descrita per cada punt de la meridiana és anomenada parallel Els meridians i els parallels d’una superfície esfèrica són circumferències Els meridians de la superfície terrestre són aproximadament ellipses
teorema central del límit
Matemàtiques
Teorema segons el qual, per a una distribució de probabilitat arbitrària de mitjana μ i variància σ2, i essent x̄ la mitjana de n observacions independents d’aquesta distribució, la variable
té una distribució
.
Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/ n de la d’aquesta A la pràctica, per a n ≥ 10 l’aproximació és ja suficient Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries Això explica per què a la pràctica hi ha moltes variables que segueixen una…
fórmula de Stirling
Matemàtiques
Expressió matemàtica que permet de calcular, aproximadament, el factorial d’un nombre n, si és molt més gran que 1.
L’exactitud del resultat és tant més bona com més gran és n Hom l’escriu Val a dir que, per a qualsevol valor de n , es compleix
símbol
Matemàtiques
Lletra o signe gràfic de qualsevol mena utilitzat per a representar quantitats (nombres), relacions o operacions.
Cal distingir sempre el símbol del concepte Així, el nombre dos concepte pot ésser representat per símbols diferents 2, II, ╫, etc Principals símbols símbols emprats en teoria de conjunts ∈ pertany a ∉ no pertany a = igual a ≠ diferent ⊂ inclusió, és inclòs en ⊄ no és inclòs en ⋂ intersecció ⋃ reunió − diferència ∁ , − , ∽ complementari ∆ diferència simètrica → aplicació, funció ≃ coordinable, bijectiu x producte cartesià {} singletons claudàtors ∅ conjunt buit ℕ nombres naturals ℤ nombres enters ℚ nombres racionals ℝ nombres reals ℂ nombres complexos símbols…
angle
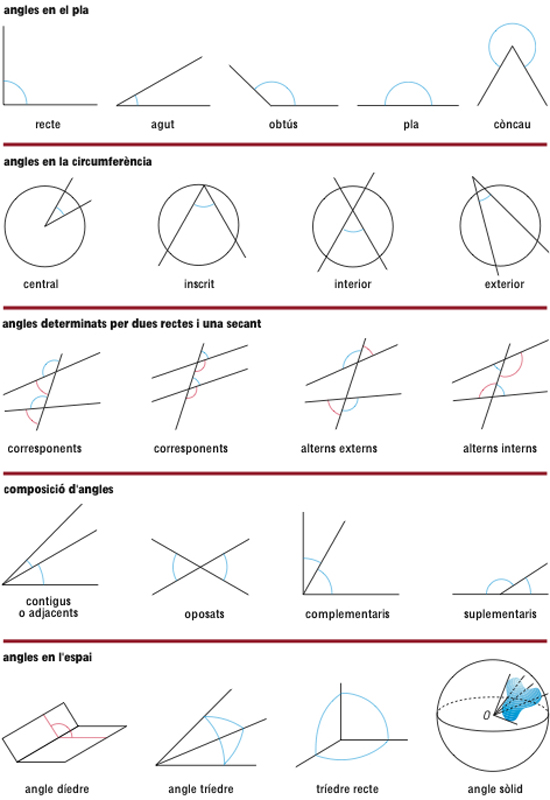
Diversos tipus d’angles
© Fototeca.cat
Matemàtiques
Regió del pla limitada per dues semirectes d’origen comú.
Per a mesurar angles hom utilitza diverses unitats l’angle recte, el grau sexagesimal, el grau centesimal i el radian El grau sexagesimal és obtingut dividint el cercle en 360 parts iguals El grau es divideix en 60 minuts i el minut en 60 segons Les abreviatures són ° grau, ′ minut, ″ segon Per exemple, 23° 27′ 35″ es llegeix 23 graus , 27 minuts i 35 segons El transportador d’angles permet fer mesures directes d’angles dibuixats en graus sexagesimals El grau centesimal és obtingut dividint l’angle recte en 100 parts iguals El grau es divideix en 100 minuts i el minut en 100 segons El símbol…
correlació
Matemàtiques
Grau d’interdependència entre diverses variables o, dit d’una altra manera, entre diferents conjunts de nombres.
Si els valors de les diferents variables satisfan exactament una equació, hom diu que hi ha una correlació perfecta entre elles Quan hi ha dues variables, és anomenada correlació simple , i si el nombre de variables és superior a dues, correlació múltiple Donades dues variables aleatòries X , Y , la localització dels parells de punts X, Y damunt un sistema de coordenades rectangular rep el nom de diagrama de dispersió Si tots els punts del diagrama semblen trobar-se aproximadament damunt una recta, hom diu que la correlació és lineal quan els punts descriuen amb una certa…
interpolació
Matemàtiques
Procediment que, donats els n valors y 1, y 2, ..., yi, ..., yn d’una funció y = g(x) en els punts x 1, x 2..., xi, ..., xn, permet de calcular, aproximadament, els valors de g(x) en punts intermedis als donats.
Més exactament, la interpolació consisteix a trobar una altra funció y = f x , d’un tipus escollit, que passi pels punts x i , y i Una primera aproximació és constituïda per la interpolació lineal , que consisteix a imposar que, entre cada dos punts consecutius dels donats, f x sigui un segment de recta En la interpolació de Lagrange , f x és un polinomi de grau n- 1 donat per la fórmula Si els punts x i constitueixen una progressió aritmètica, és emprada la interpolació de Newton càlcul de diferències diferència
aritmètica
Matemàtiques
Estudi dels nombres naturals i de les operacions d’addició, subtracció, multiplicació, divisió entera, potenciació i extracció d’arrels enteres entre aquests nombres.
L’aritmètica ha nascut a totes les civilitzacions ensems amb el llenguatge per anomenar conjunts de persones o d’objectes i després per facilitar els intercanvis comercials Els egipcis s’havien ocupat d’alguns problemes aritmètics, i les obres que n'han estat conservades la més antiga de les quals és el papir Rhind ~s XVII aC contenen la resolució d’algunes qüestions numèriques sense dir en quines propietats recolza la resolució, ni menys encara justificar-les El nivell de llurs coneixements era, aproximadament, el de l’actual ensenyament primari, però eren enunciats amb un llenguatge més…