Resultats de la cerca
Es mostren 8 resultats
políedre
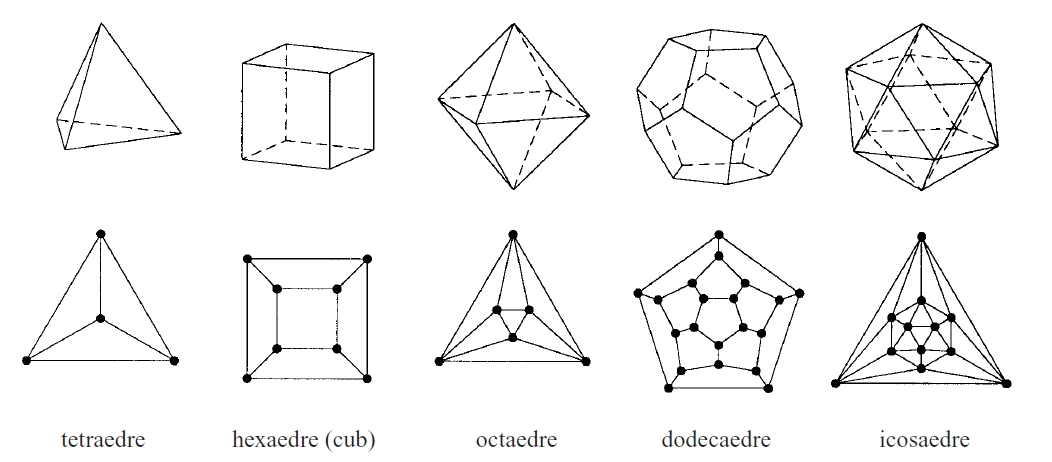
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…
propietat universal
Matemàtiques
Relació o propietat que caracteritza o defineix un objecte matemàtic d’una manera unívoca (a part un isomorfisme trivial).
Així, els grups simètrics associats a conjunts que tenen una llei de composició interna resten caracteritzats per una propietat universal
distribució
Matemàtiques
Conjunt de dades o valors les freqüències dels quals són indicades per mitjà dels tants per cent en què es presenten o bé de forma absoluta, segons una escala predeterminada.
Dins l’estadística teòrica aquests valors són associats a probabilitats, la distribució de les quals és estudiada mitjançant la funció de distribució
Elwin Bruno Christoffel
Matemàtiques
Matemàtic alemany.
Treballà especialment en el camp de la geometria diferencial Introduí els símbols que duen el seu nom símbols de Christoffel associats a la forma quadràtica gμν, símbols que apareixen en la relativitat general
Ronald Aylmer Fisher
Matemàtiques
Matemàtic estadístic anglès, considerat com el creador de l’estadística moderna.
A partir del 1919 treballà a l’estació experimental de Rothamsted, on desenvolupà un nou enfocament matemàtic de l’estadística amb tests exactes de significació per a mostres petites i una teoria de l’estimació que els és aplicable, el mètode de la màxima versemblança, les bases de la moderna planificació d’experiències i els mètodes d’anàlisi associats anàlisi de la variància Féu recerques en genètica i eugenèsia, que el portaren a ocupar la càtedra Galton d’eugenèsia, després de K Pearson, a la Universitat de Londres, i la de genètica a la de Cambridge 1943-57 Publicà, entre…
translació
Matemàtiques
Transformació geomètrica que a cada punt M
del pla n’hi associa un altre M’
de manera que el vector de manera que el vector
sigui un representant d’un vector lliure
prefixat, anomenat vector de la translació
Les translacions són isometries que en el pla conserven el sentit de les rotacions i en l’espai el caràcter dels tríedres, no tenen punts dobles i en les quals les rectes i els plans parallels al vector de translació són invariants El conjunt de totes les translacions del pla o de l’espai formen un grup commutatiu amb l’operació composició, el qual és isomorf al grup additiu dels vectors lliures ordinaris associats al pla o a l’espai considerat Si és el vector característic d’una translació, el punt transformat d’un punt M x 1 ,x 2 ,x 3 és el punt M' x' 1 ,x' 2 ,x' 3 , les…
intuïcionisme
Matemàtiques
Corrent del pensament matemàtic, nascut a la segona meitat del s XIX.
Propugna que la matemàtica és l’estudi d’uns tipus de construccions mentals en les quals els objectes que hom maneja han d’ésser definits donant un criteri que en permeti la construcció i on el llenguatge emprat, sigui ordinari o simbòlic, només és un instrument auxiliar i no una part essencial de les construccions formalisme Hom accepta que la matemàtica intuïcionista és formada de tot allò que és conseqüència segons les normes de la lògica intuïcionista de la construcció de la successió dels nombres naturals ℕ, de la qual resulten evidents els axiomes de Peano base de la construcció formal…
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que conté la…