Resultats de la cerca
Es mostren 7 resultats
curtosi
Matemàtiques
Grau d’apuntament d’una distribució estadística, és a dir, grau de convexitat o aplatament de la corba representativa d’una distribució estadística.
La curtosi β 2 és mesurada, generalment, mitjançant l’expressió β 2 =μ 4 /μ 2 2 on μ 2 i μ 4 són els moments d’ordre 2 i 4, respectivament Atès que β 2 ≃3 per a una distribució normal, hom pren, correntment, com a mesura de la curtosi, el terme K= β 2 -3 Una distribució és leptocúrtica si K > 0 , mesocúrtica si K = 0 i platicúrtica si K < 0
endomorfisme
Matemàtiques
Aplicació d’una certa estructura algèbrica E en ella mateixa, conservant-la.
Hom pot demostrar que el conjunt d’endomorfismes sobre una mateixa estructura té l’estructura d’espai vectorial si hom defineix la suma i el producte d’endomorfismes d’altra banda, llur conjunt adquireix l’estructura d’anell, el qual és isomorf al de les matrius quadrades d’ordre n , atès que cada endomorfisme pot ésser caracteritzat per una matriu Definida una funció determinant no degenerada a E , hom anomena determinant d’un endomorfisme el determinant de la matriu que el representa referida a qualsevol base També pot éser demostrat que el determinant del producte de dos endomorfismes és…
mètode dels multiplicadors de Lagrange
Matemàtiques
Mètode per a trobar els màxims o mínims d’una funció u = F(x1, x2,..., xn) de n variables, les quals són sotmeses a k condicions suplementàries φ1(x1, x2,..., xn) = 0, φ2(x1, x2,..., xn) = 0,..., φk(x1, x2,..., xn) = 0.
, x n = 0, φ 2 x 1 , x 2 ,, x n = 0,, φ k &x 1 , x 2 ,, x n = 0 El mètode consisteix a formar la funció + λ 2 φ 2 x 1 ,, x n + λ 2 φ 2 > x 1 ,, x n , + + λ k φ k x 1 ,, x n , on λ 1 ,, λ k són constants indeterminades, anomenades multiplicadors de Lagrange les n derivades parcials de ϕ igualades a 0 juntament amb les k condicions constitueixen un sistema de n + k equacions i n + k incògnites λ 1 ,, λ k , x 1 , , x n Atès que aquest sistema constitueix només una condició necessària que la solució del problema ha de satisfer, cal comprovar, un cop resolt el sistema, si els…
discontinuïtat
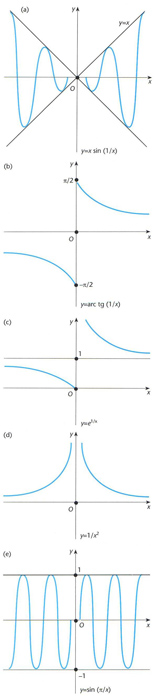
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…
teoria de la computació
Matemàtiques
Branca de les matemàtiques que estudia problemes de decidibilitat.
Com és usual en la història de les matemàtiques, té orígens aparentment molt diferents que finalment conflueixen i permeten d’establir el que esdevé una teoria enormement potent i irrenunciable Cal remarcar-ne el problema diofàntic plantejat per David Hilbert l’any 1900, i el problema de les paraules que sorgí en el món de la topologia algèbrica Es tracta de dos problemes típics de decidibilitat és a dir, aquells en què cal disposar d’un mètode que permeti de decidir una o altra de dues opcions atesa una equació diofàntica, té solució, són equivalents dues paraules donades per endavant L’any…
matemàtica
Matemàtiques
Ciència que estudia les propietats dels nombres, de les figures, dels conjunts, de les operacions, de les funcions, etc.
Aquesta definició és força descriptiva, però incompleta, i per això diversos matemàtics han intentat de definir la matemàtica tot assenyalant-ne els trets més característics Així, segons B Russell, la matemàtica consisteix només en afirmacions tals com “si una proposició és veritable referida a un objecte, aleshores una altra proposició també ho és”, de manera que la matemàtica és aquell camp en què hom no sap mai de què parla ni si allò que diu és veritat o no Dins aquesta mateixa línia, H Poincaré diu que els matemàtics no estudien objectes, sinó relacions entre objectes no els interessa la…
àlgebra

Triàngle numèric, més tard conegut com a triangle de Pascal, d’un manuscrit xinès del 1303
© Fototeca.cat
Matemàtiques
Branca de les matemàtiques que estudia les estructures algèbriques dels conjunts.
Hom l’aplica, per tant, en les situacions on hi ha un conjunt ben definit i una noció clara d’operació entre els seus elements operació interna o entre aquests i els elements d’altres conjunts operació externa L’àlgebra ha evolucionat des de l’interès inicial per a resoldre problemes fonamentalment pràctics fins al desenvolupament del mètode abstracte Dues inclinacions diferents han desembocat en l’àlgebra moderna D’una banda, l’ àlgebra clàssica , simple instrument per a fer càlculs i resoldre equacions que usava només els conceptes immediats que hom reconeixia al problema les quantitats…