Resultats de la cerca
Es mostren 9 resultats
cadena
Matemàtiques
Successió de variables aleatòries tal que la distribució de probabilitat d’una d’elles depèn dels valors obtinguts per les anteriors.
cadena de Markov
Matemàtiques
Seqüència d’experiències aleatòries ξ1, ξ2,..., ξn...tal, que la probabilitat condicional de ξn, coneguts els resultats de les experiències anteriors, és igual a la probabilitat condicional de ξn quan hom coneix només el resultat immediatament anterior.
Andrej Andrejevič Markov
Matemàtiques
Matemàtic rus, deixeble de P.L. Čebyšev.
Fou un dels membres més destacats de l’escola de matemàtics russos dedicats a l’estudi de la teoria de probabilitats Treballà especialment en la llei dels grans nombres, i analitzà els processos estocàstics, els quals considerà com una cadena de proves, que ha estat anomenada cadena de Markov Aplicà els seus coneixements matemàtics a la lingüística anàlisi de Markov per a estudiar la freqüència dels mots i de llurs encadenaments
René Maurice Fréchet
Matemàtiques
Matemàtic probabilista francès.
Dedicat inicialment a l’estudi dels espais abstractes, reestructurà certs capítols de les matemàtiques per mitjà d’alguns axiomes emprant el llenguatge de la geometria distància, separació, entorn Encarregat per Borel de l’ensenyament del càlcul de les probabilitats a Estrasburg, s’especialitzà en aquesta teoria i esdevingué un dels capdavanters de la presentació axiomàtica de la probabilitat publicà obres sobre la noció de variable aleatòria i les formes de convergència de la teoria de les probabilitats i sobre les probabilitats en cadena
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta cadena…
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema si aquestes…
demostració
Lògica
Matemàtiques
Derivació d’un enunciat, mitjançant l’aplicació d’unes determinades regles lògiques, a partir d’uns altres enunciats, dits premisses de la demostració.
Qualsevol cadena de demostracions ha d’arrencar d’un conjunt finit de premisses no demostrables, els axiomes Aquest conjunt és anomenat el sistema dels axiomes de la teoria deductiva, i els enunciats que són demostrats a partir dels axiomes s’anomenen teoremes Identificada, en la teoria platònica, amb la definició, Aristòtil la considerà com un procés superior, adreçat a extreure, mitjançant el sillogisme, una conclusió a partir d’unes premisses certes L’escolàstica s’adherí a l’esquema aristotèlic i n'elaborà una classificació propter quid , ad intellectum , ad sensum , a…
catenària
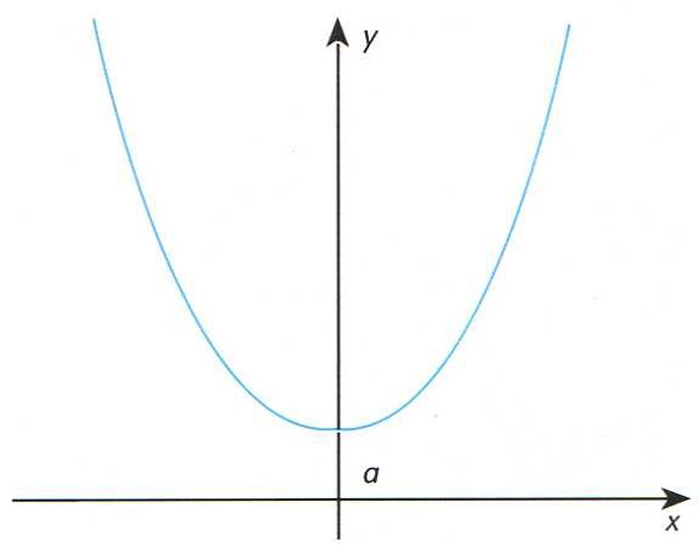
La major o menor concavitat de la corba depèn de la separació dels punts extrems (que es determinen pel paràmetre a de la seva equació)
© fototeca.cat
Matemàtiques
Corba que adopta una cadena, corda, etc, perfectament flexible i amb una càrrega uniformement repartida en tota la seva llargària, fixa en els seus extrems i suspesa lliurement.
L’expressió matemàtica d’aquesta corba és donada per l’equació y=achx/a , on a és la distància des del punt més baix de la corba a l’eix d’abcisses de referència