Resultats de la cerca
Es mostren 12 resultats
arrel d’una equació
Matemàtiques
Valor de la quantitat desconeguda que satisfà l’equació.
És anomenada també solució o zero de l’equació Per exemple, en l’equació el valor 1 és una arrel, car en substituir x per 1 el membre de l’esquerra s’anulla Hom empra el mot arrel, car les solucions de les equacions de grau baix, llevat de les de primer grau, es resolen comunament emprant radicals
zero
Matemàtiques
Nom de la xifra 0, numeral cardinal que designa l’absència d’unitats.
El zero és l’element neutre en la suma de nombres enters, ja que a + 0 = a , per a tot a Les regles algèbriques del zero són a + 0 = a a 0 = 0 0/ a = 00 si a ≠ 0 0 = 1 Les expressions a /0 i 0/0 són indeterminades ja que 0/0 = 1, car 0 = 1 0, però també 0/0 = 2, car 0 = 2 0, etc, és a dir, que el zero no pot dividir mai El nombre zero i la xifra zero és una creació de la cultura hindú Āryabaṭha, Brāhmagupta, Bhāskara, etc, que cap al segle V dC fou introduït conjuntament amb el sistema decimal de numeració posicional, sistema que els àrabs incorporaren al seu coneixement i divulgaren com…
Pierre Gassendi
Filosofia
Física
Matemàtiques
Cristianisme
Clergue; matemàtic, físic i filòsof materialista francès.
Estudià teologia, grec i hebreu a Ais de Provença i es doctorà en teologia a Avinyó Fou professor 1645 al Collège Royal de París És conegut pels seus atacs a la filosofia dels aristotèlics, que considera com a purament verbal, car, per a ell, la veritable ciència ha de partir de les qualitats experimentals de les coses Fonamenta el coneixement en una doctrina sensualista i en l’atomisme clàssic de Demòcrit i Epicur Fou amic de Hobbes, entusiasta de Galileu, Copèrnic i Kepler i contradictor de l’intellectualisme cartesià Escriví llibres de física, matemàtiques, astronomia i…
paradoxa
Lògica
Matemàtiques
Enunciat o raonament que porta a dues conclusions mútuament contradictòries però de cap de les quals hom no pot prescindir.
Sovint identificable amb l'antinòmia i àdhuc amb l'aporia, la paradoxa, que té un significat més ampli que l’una i l’altra, sol ésser tipificada en l’afirmació del mentider, quan diu “ara dic mentida” si és veritat que diu mentida, és que menteix, però està dient la veritat, o sia que no està mentint i, si no és veritat que diu mentida, menteix, però no és veritat que digui mentida Les paradoxes d’aquesta mena, consistents en una autoreferència i que solen ésser típiques en les anomenades paradoxes semàntiques o lingüístiques, han estat estudiades des de sempre i hom només ha pogut trobar-ne…
perspectiva cavallera
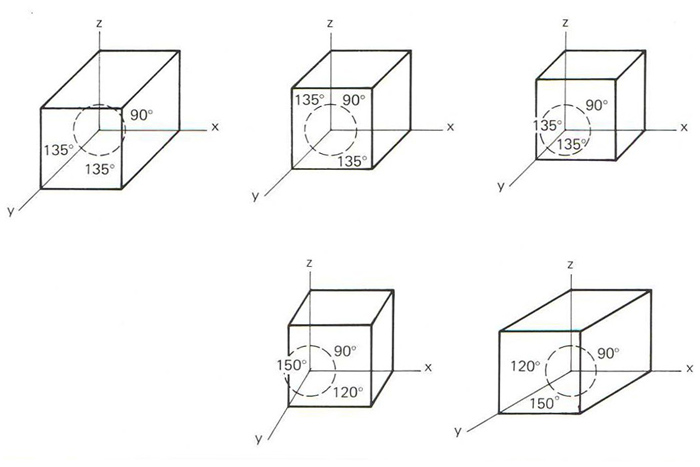
Representació d’un cub amb diferents reduccions i angles
© fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Projecció cilíndrica obliqua d’un cos sobre el pla de projecció (pla del quadre).
En aquest cas el pla del quadre és el mateix pla coordenat OXZ, i per això les rectes paralleles als eixos OZ i OX es projecten en llur veritable magnitud L’eix Y és projectat en el quadre amb una direcció dependent de la que tinguin les projectants, i sofreix, per tant, la reducció Per a les representacions en aquest sistema, caldrà conèixer la reducció de l’eix Y i el valor de l’angle XOY o YOZ, que oscillarà entre 0º i 360º aquesta relació serà constant per a totes les línies paralleles a l’eix Y L’angle que forma l’eix Y amb l’eix X podria ésser elegit indistintament, però evitant els…
programació matemàtica
Matemàtiques
Conjunt de procediments matemàtics per a resoldre problemes d’òptims condicionats, és a dir, problemes consistents a maximitzar o minimitzar una funció numèrica de diverses variables subjectes a certes limitacions.
Comprèn la programació lineal i les seves aplicacions transport, paramètrica, estocàstica, de nombres enters, la programació quadràtica denominada d’acord amb el grau de les equacions que cal optimitzar i la programació dinàmica , que es refereix més a la técnica computacional que no pas a un tipus particular de problema no lineal Aquestes tècniques tenen un origen recent Sembla que la programació lineal fou emprada per Monge, el 1776, però no fou coneguda fins el 1939, que l’economista soviètic LVKantorovič la descobrí La situació política impedí el desenvolupament i la difusió d’aquesta…
Josep Vicent de l’Olmo i Conca
Literatura catalana
Matemàtiques
Arqueologia
Història
Generós i secretari del Tribunal del Sant Ofici de la Inquisició de la seva ciutat natal, s’interessà per la matemàtica i per la poesia.
Succeí el seu pare com a secretari del tribunal de la inquisició de València La seva fama d’home assenyat el convertí en conseller polític de la ciutat —el 1661 formà part del consell general—, segons informen alguns dels seus contemporanis Formà part d’acadèmies de matemàtiques —fou membre de l’acadèmia de l’Alcàsser i el 1685 de la que presidia el comte d’Alcúdia Onofre Vicent Escrivà d’Íxer, on parlà diverses vegades sobre l’esfera— i com a poeta també participà en diversos certàmens religiosos Guanyà el primer premi de poesia als certàmens dels anys 1665, 1667 i 1668, sempre amb…
, ,
nombre
Matemàtiques
Resultat de comptar les coses que formen un agregat (dos, tres, quatre, etc., i també un, o sia, la unitat) o qualsevol dels ens abstractes que resulten de generalitzar aquest concepte.
El concepte de nombre ha anat evolucionant al llarg de la història així, al principi anava enllaçat amb el simple ús de xifres o guarismes per a comptar sistemes de numeració Els nombres 1, 2, 3, 4, etc, ja eren usats en les antigues cultures babilònica, egípcia, xinesa la qual coneixia els negatius i índia la qual introduí el zero Aquest ús de xifres no implicava, però, cap concepte abstracte de nombre A l’antiga Grècia els pitagòrics consideraren que el nombre era una estructura determinada, immanent a totes les coses això generà la numerologia grega o mística, basada en les…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
geometria
Matemàtiques
Part de la matemàtica basada en la intuïció d’espai.
El nom prové de la seva primera aplicació la mesura de la Terra Els diversos apartats en què hom divideix la geometria fan referència a la natura dels objectes d’estudi i al mètode emprat Per a una definició unitària de la geometria elemental, l’any 1872 CF Klein proposà,en el “programa d’Erlangen”,la noció de geometria com a consideració d’un espai el conjunt dels punts i un grup de transformacions d’aquest espai, els invariants del qual serien les nocions de la geometria en qüestió El primer estudi de la geometria fou de caràcter intuïtiu, i consistí en la compilació de fets relatius a…