Resultats de la cerca
Es mostren 19 resultats
relació d’equivalència
Matemàtiques
Relació binària entre els elements d’un conjunt que permet d’establir una classificació d’aquests elements de tal manera que resti cadascun en una classe, dita d’equivalència, i aquestes classes no tinguin cap element comú.
Perquè una relació sigui d’equivalència cal que sigui reflexiva, simètrica i transitiva relació Tota relació d’equivalència estableix una classificació del conjunt i tota classificació determina una relació d’equivalència Són equivalents dos elements que pertanyen a la mateixa classe El conjunt de les classes considerada cadascuna com un nou element és anomenat conjunt quocient del conjunt de partida C per a aquesta relació R , i s’escriu C/R Una aplicació d’un conjunt en un altre determina una relació d’equivalència entre els elements del conjunt original, prenent…
teorema de Rouché-Frobenius
Matemàtiques
Teorema que permet la classificació dels sistemes lineals d’equacions.
Donat un sistema no homogeni de m equacions lineals amb n incògnites, escrit en forma matricial A x = b , b ≠ 0 , on A és la matriu de coeficients del sistema, b la columna dels termes independents i x la columna de les incògnites, el sistema és compatible és a dir, que té solucions si el rang de A és igual al rang de la matriu ampliada A , b matriu Si aquest rang és igual al nombre d’incògnites, aleshores es tracta d’un sistema compatible determinat o sia, amb solució única, però si el rang és menor que el nombre d’incògnites, es tracta d’un sistema compatible indeterminat amb infinites…
gènere d’una corba
Matemàtiques
Nombre que, segons una certa classificació, correspon a una corba algèbrica.
Per a les corbes planes el gènere g és donat per l’expressió n essent-hi l’ordre o grau de la corba i μ x l’ordre de multiplicitat de cadascun dels punts múltiples de la corba
dendrograma
Matemàtiques
Diagrama en forma d’arbre que mostra relacions de proximitat entre els individus representats.
És un dels mètodes de representació jeràrquica més emprats en estadística, classificació automàtica, etc
John G. Thompson
Matemàtiques
Matemàtic nord-americà.
Féu contribucions importants per a la classificació dels grups finits, en demostrar que tot grup finit simple no cíclic conté un nombre parell d’elements Medalla Fields 1970 i premi Abel 2008
signatura
Matemàtiques
Nombre de termes positius en una forma quadràtica reduïda a una suma de quadrats mitjançant una transformació lineal.
La signatura d’una matriu simètrica és el nombre de termes positius que apareixen en diagonalitzar la matriu Amb el rang , la signatura constitueix un dels invariants fonamentals en la classificació de les matrius corresponents a les còniques i a les quàdriques
Maurice d’Ocagne
Matemàtiques
Matemàtic francès.
Aplicà la geometria als càlculs numèrics i pot ésser considerat com el creador de la nomografia, els principis de la qual exposà en el seu Traité de nomographie 1899 Estudià els principis de les màquines de calcular, de les quals féu una classificació comparativa
Shigefumi Mori

Shigefumi Mori
© International Mathematical Union
Matemàtiques
Matemàtic japonès.
Graduat a la Universitat de Kyoto l’any 1975, es doctorà el 1978 amb una tesi sobre l’endomorfisme dels anells en variants abelianes Posteriorment fou professor assistent en aquesta universitat fins el 1980, que passà a la Universitat de Nagoya, on fou nomenat professor titular el 1988 L’any 1990 retornà a la Universitat de Kyoto, on ocupa una càtedra Des del 1977 ha estat professor visitant en diverses universitats dels EUA El seu interès se centra en la geometria algèbrica, i ha desenvolupat tècniques per tal de resoldre el problema de la classificació completa de les varietats…
‘Umar Ḫayyām
Astronomia
Literatura
Matemàtiques
Poeta, matemàtic i astrònom persa.
Visqué a la cort del seljúcida Malik Šāh , el visir del qual, Niẓām al-Mulk, li encomanà la creació i la direcció d’un observatori astronòmic a Merv Reformà el calendari iranià reduint l’antic any solar persa al lunar musulmà És autor, en àrab, de dos tractats de filosofia i de ciències de la natura i de notables obres algèbriques mètode per a l’extracció d’arrels quadrades i cúbiques, classificació d’equacions de segon i de tercer grau segons el nombre dels termes que contenen —bé que no arribà a resoldre ni les imaginàries ni les negatives—, etc Assolí, però, la màxima fama com…
cònica
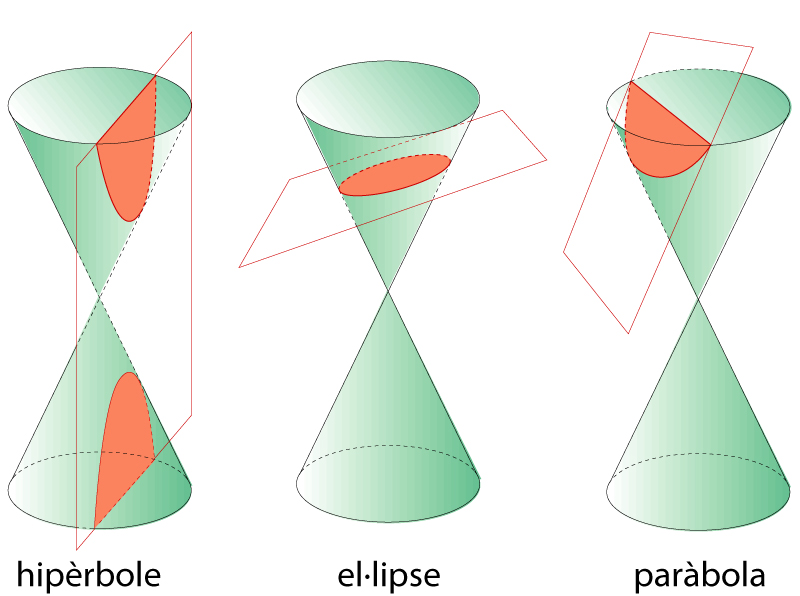
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…