Resultats de la cerca
Es mostren 13 resultats
angle complet
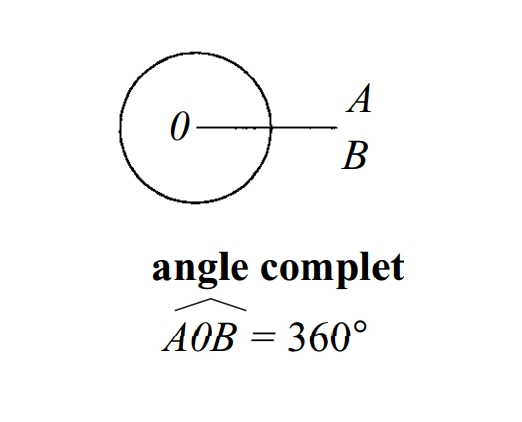
angle complet
espai complet
Matemàtiques
Espai topològic on tota successió de Cauchy convergeix vers un punt de l’espai.
quadrilàter complet
Matemàtiques
Figura formada per quatre rectes que es tallen dos a dos determinant sis punts d’intersecció.
espai de Banach
Matemàtiques
Espai vectorial normat complet.
És, doncs, un espai vectorial on hi ha definida una norma espai normat per a la qual tota successió de Cauchy convergeix
espai de Hilbert
Matemàtiques
Espai prehilbertià complet (successió de Cauchy).
Els espais euclidians clàssics → n amb el producte escalar habitual són espais de Hilbert
al-Bīrūnī
Astronomia
Matemàtiques
Matemàtic, astrònom i metge d’origen persa.
El seu nom complet era Abū al-Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī Pertanyia a la secta heterodoxa i al grup de la šu'cubiyya pobles no àrabs, defensor de la igualtat de tots els musulmans És autor de llibres d’astronomia i d’astrologia i de Ta'riḫ al-Hind ‘Història de l’Índia’
successió de Cauchy
Matemàtiques
Successió {Xn} en que la distància entre dos termes, d(xm,xn)>, tendeix a zero quan m,n tendeixen a infinit.
El seu significat és donat un nombre qualsevol ε> 0, existeix un N tal que dx m ,x n > ε quan m,n > N Cal fer notar que tota successió convergent és successió de Cauchy, tenint en compte, tanmateix, que no tota successió de Cauchy és convergent en l’espai mètric de tots els nombres reals, en el qual d α,β = α-β, tota successió de Cauchy és convergent Aquest és un exemple d’un tipus important d’espais mètrics l’espai mètric complet , definit com un espai mètric en el qual tota successió de Cauchy és convergent
axiomatització
Filosofia
Matemàtiques
Utilització, per part d’una ciència, d’una estructura formalitzada o sistema purament abstracte i formal, que parteix d’uns axiomes o postulats i s’expressa en un simbolisme el més precís possible (axiomàtica).
L’axiomatització té la seva aplicació sobretot en lògica i matemàtiques L’axiomatització d’una ciència pot ésser feta de diverses maneres, puix que per a cada una hi ha diversos sistemes d’axiomes equivalents L’elecció d’un sistema d’axiomes o altre depèn del fi de base crítica dels fonaments, exposició didàctica, aplicacions tècniques, etc Una de les tendències de la lògica actual és de descobrir els mètodes més precisos d’axiomatització i una teoria completa dels símbols lògics per poder fomalitzar tant com sigui possible tots els sistemes L’axiomatització d’una teoria pressuposa tenir-ne…
residu
Matemàtiques
Solució a de la congruència Xn ≡a (mòdul m).
Així, hom diu que 4 és el residu en la congruència 3 2 ≡4 mòdul 5 Qualsevol conjunt d’enters que té la propietat que dos elements no pertanyen a la mateixa classe numèrica mòdul n és anomenat un sistema complet residual mòdul n Així 1, 9, 3-3, 5-1, 7 és un sistema d’aquest tipus respecte al mòdul 7 Dos nombres a, b són congruents mòdul n —que hom representa a ≡b mòdul n — si a-b és un múltiple de n o, equivalentment, si b és el residu de dividir a per n fixat n , els valors possibles que hom pot obtenir per a b són anomenats residus , i el conjunt que determinen és anomenat…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica, però, hom pren…