Resultats de la cerca
Es mostren 47 resultats
nombre complex
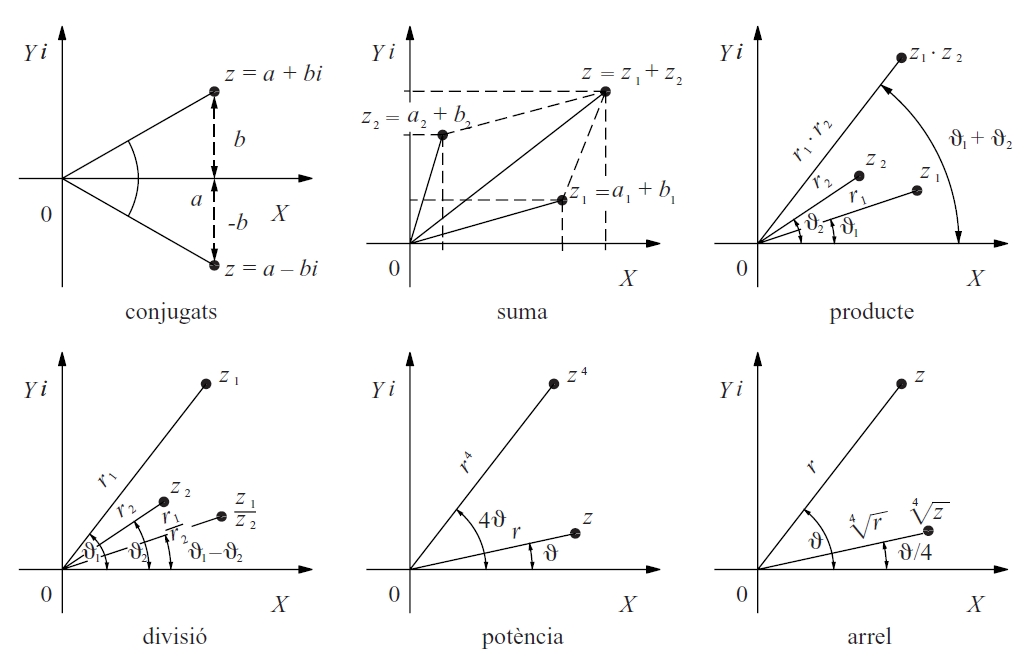
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta…
cos complex
Matemàtiques
L’equació quadràtica x2 + 1 = 0 no té solució en el cos ℝ dels nombres reals.
Cal, doncs, construir un cos que contingui el cos ℝ com a subcòs i alhora un element i que compleixi i 2 + 1 = 0 Per fer-ho és possible procedir de dues formes D’una banda, és possible de considerar el pla complex D’una altra, és possible de considerar l’anell quocient ℂ = ℝ X / x 2 + 1, on ℝ X és l’anell dels polinomis en la variable X amb coeficients reals i X 2 + 1 és l’ideal engendrat pel polinomi, irreductible a ℝ, X 2 + 1 Hom disposa aleshores de l’aplicació canònica π ℝ X → ℂ i la imatge d’ X és anomenada i És a dir, i = π X Aquest cos té una propietat molt important…
pla complex
Matemàtiques
Pla de ℝ 2
obtingut mitjançant la identificació dels punts < x
, y
> amb els nombres complexos x
+ iy
.
Aquest pla rep també el nom de pla de Gauss o de Gauss-Argand Un punt z = < x , y > admet una representació en coordenades polars i, per tant, z = ρ ⋅ cos θ + i ⋅ sin θ que, d’acord amb la identitat d’Euler, hom escriu z = ρ ⋅ e i⋅θ Aquesta expressió permet de calcular amb facilitat les potències dels nombres complexos i extreure'n les seves arrels n -èsimes Resulta aleshores que la fórmula de Moivre s’expressa
funció sinus complex
Matemàtiques
Funció sin: ℂ→ℂdefinida per l’assignació z →(eiz-e-iz)/2i.
És una de les sis funcions trigonomètriques complexes
funció cosinus complex
Matemàtiques
Funció cos: ℂ→ℂdefinida per l’assignació z →(eiz + e-iz)/2.
És una de les sis funcions trigonomètriques complexes
funció cosinus hiperbòlic complex
Matemàtiques
Funció ch: ℂ→ℂdefinida per l’assignació z →(ez + e-z)/2, on ez és la funció exponencial complexa.
Se satisfà que ch z = cos iz i que cos z = ch iz , on cos és la funció cosinus complex
funció sinus hiperbòlic complex
Matemàtiques
Funció sh: ℂ→ℂdefinida per l’assignació z → (ez-e-z)/2, on ez és la funció exponencial complexa.
Se satisfà que sh z = -i sin iz i que sin z = 1/ i ch iz , on sin és la funció sinus complex
mòdul d’un nombre complex
Matemàtiques
Donat un nombre complex, z=a+ib, arrel quadrada de a 2+b 2
.
És denotat per | z | Satisfà que | z | 2 = zz , on z és el complex conjugat de z
argument d’un nombre complex
Matemàtiques
Angle format pel segment que uneix l’origen amb l’afix del nombre complex considerat i l’eix real.