Resultats de la cerca
Es mostren 6 resultats
mètode de racionalització de Gauss
Matemàtiques
Algorisme emprat en l’estudi dels espais vectorials que, donats uns vectors arbitraris, permet de deduir-ne efectivament els que són linealment independents i que, per tant, també són base del subespai que generen.
Hom aplica aquest mètode per a trobar el rang d’una matriu qualsevol no necessàriament quadrada, considerant cada fila de la matriu com un vector
angles de direcció
Matemàtiques
Qualsevol dels tres angles positius que té una recta orientada que passa per l’origen respecte dels tres semieixos positius de referència a l’espai.
Els angles de direcció es poden calcular per a qualsevol recta, considerant la parallela corresponent que passa per l’origen En tot cas, cal fixar-ne la direcció
cicloide
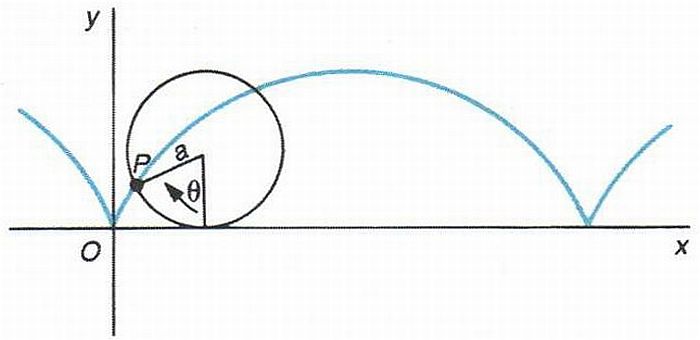
Cicloide
©
Matemàtiques
Corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una recta.
Les seves equacions paramètriques són x = a θ - sinθ, y = a 1 - cosθ Hom pot ampliar aquesta definició considerant una trajectòria fixa en lloc d’una recta així, per exemple, l' epicicloide és la corba engendrada per un punt fix en una circumferència que rodola, sense lliscar, damunt una altra circumferència i exteriorment a ella
Ruggero Giuseppe Boscovich
Astronomia
Física
Matemàtiques
Físic, astrònom i matemàtic italià, d’origen croat.
Cursà estudis de física i matemàtiques al Collegium Romanum, i el 1726 entrà a la Companyia de Jesús En collaboració amb Christopher Mainer amidà l’arc de meridià entre Roma i Rímini 1750-53 En ésser els jesuïtes expulsats d’Itàlia el 1773, anà a París per invitació de Lluís XIV, on li fou concedida la direcció del departament d’òptica naval fins el 1782, que tornà a Itàlia A la seva obra fonamental, Theoria philosophiae naturalis redacta ad unicam legem virium in natura existentium Viena, 1758, criticà els conceptes fonamentals de l’obra de Newton, considerant-los similars als…
sumabilitat de Cesaro
Matemàtiques
Generalització natural de la sumabilitat usual de les sèries, la qual engloba com un cas especial, definida considerant la successió de mitjanes aritmètiques de les sumes parcials.
El terme general és donat per l’expressió ν ν = 1/n u 1 + u 2 + + u n Hom diu que la sèrie { u n } és sumable en el sentit de Cesaro si la successió ν ν convergeix Qualsevol sèrie convergent en el sentit usual és sumable en el sentit de Cesaro, i la suma dóna el mateix valor però, a més, moltes sèries divergents en el sentit usual, com per exemple la sèrie u n = - 1 n , són sumables en el sentit de Cesaro
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats aplicables a grups…