Resultats de la cerca
Es mostren 22 resultats
equació diferencial de Cauchy
Matemàtiques
Equació diferencial lineal amb coeficients variables de forma:
on p0, p1...pn són constants.
Pot ésser transformada en una equació diferencial lineal amb coeficients constants mitjançat el canvi x=e z Aquesta equació és molt emprada en l’estudi de circuits elèctrics i problemes d’estabilitat
augmentar
Matemàtiques
Ampliar el nombre de condicions, equacions, variables, constants, axiomes, etc.
variable
Matemàtiques
En una expressió matemàtica, símbol que representa una quantitat el valor numèric de la qual no és especificat.
En una expressió matemàtica qualsevol, hom pot distingir quatre elements bàsics els símbols operatius, els nombres, les constants i les variables Així, en l’expressió ax +b=0, els símbols operatius són + i =, el nombre és el 0, les constants són a i b i la variable és x La diferència entre constants i variables és la següent hom admet que, en l’esmentada expressió, les constants a i b tenen cadascuna un únic valor, fix, que no canvia al llarg del tractament matemàtic de l’expressió simplificació, aïllament de la incògnita, resolució, etc…
numèric | numèrica
Matemàtiques
Dit de l’equació en la qual els coeficients i les constants són nombres.
constant
Matemàtiques
Quantitat que té sempre el mateix valor, per exemple el nombre π.
De vegades també reben el nom de constants arbitràries els paràmetres paràmetre
sinusoide
Matemàtiques
Corba les ordenades de la qual són proporcionals als sinus de les abscisses corresponents.
L’equació general de la sinusoide és f x = A sin Bx , on A i B són constants
funcions de Bessel de primera classe
Matemàtiques
Solucions de l’equació diferencial de Bessel, de la forma
on Γ és la funció gamma.
J - n x n’és també una solució particular Si n és un nombre enter J - n x = -1 n J n x en canvi, si n no és enter J n x i J - n x són independents, de manera que la solució general de l’equació diferencial de Bessel és y x = aJ n x + bJ - n x ,en què a i b són constants
condicions inicials
Física
Matemàtiques
Donada una equació diferencial, condicions que cal imposar a la solució general per tal que prengui, ella i les seves derivades, uns determinats valors per a un valor especificat de la variable independent.
Les condicions inicials permeten, doncs, de determinar la solució particular del problema en ajustar les constants arbitràries de la solució general Per exemple, en el problema del moviment d’una massa puntual, un cop conegudes les forces que hi actuen, el moviment concret que realitza depèn només de la posició i la velocitat en un instant inicial, x t o i v t o , essent aquestes les condicions inicials del problema
paraboloide hiperbòlic
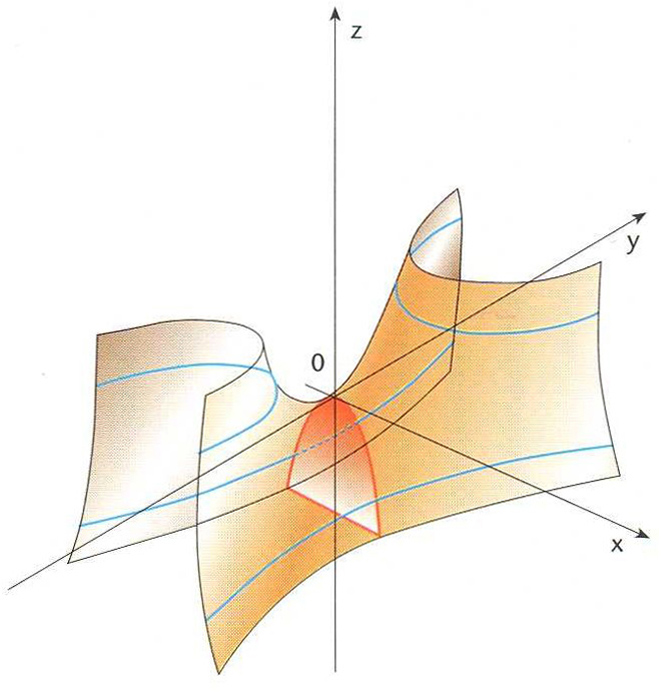
Paraboloide hiperbòlic on hi ha traçada una paràbola i dues hipèrboles
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
—
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola i la intersecció amb un pla perpendicular a l’anterior és una hipèrbola
paraboloide el·líptic
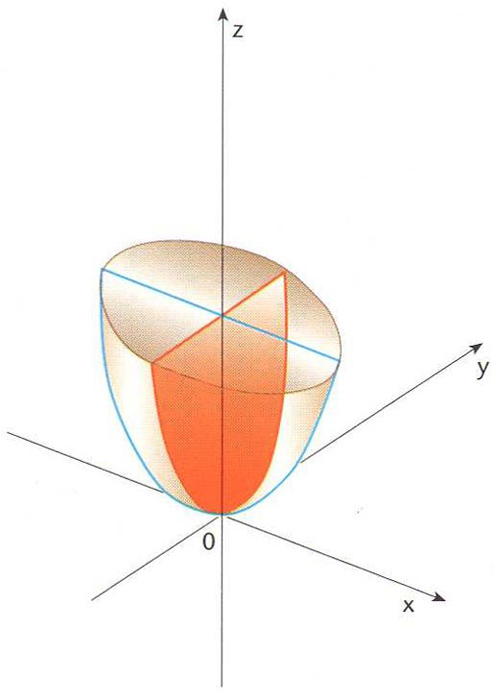
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse