Resultats de la cerca
Es mostren 15 resultats
principi de Cantor
Matemàtiques
Principi segons el qual, en la recta real, tota successió d’intervals tancats tals que cada un és contingut en l’anterior i les longituds dels quals tendeixen a zero, defineix un nombre real.
Si a n ,b n és la successió d’intervals, essent a n una successió no decreixent i b n una successió no creixent tals que la diferència b n -a n es mantingui sempre positiva, però tendint a zero quan n tendeix a infinit, el teorema de Cantor afirma que hi ha un únic nombre real x tal que x és contingut en qualsevol dels intervals a n ,b n
Teoría general de la urbanización
Matemàtiques
Obra teòrica i d’anàlisi estadística d’Ildefons Cerdà, publicada el 1867, per compte de l’Estat espanyol (reeditada en facsímil el 1968).
El primer volum inclou una història de la urbanització, un examen analític de l’estat contemporani de la urbanització, una anàlisi teoricohistòrica de les relacions entre sistemes de locomoció i formació de les urbs El segon volum correspon al títol secundari de l’obra Aplicación de sus principios y doctrinas a la reforma y ensanche de Barcelona Inclou un estudi del continent topografia, planta viària i interviària, alçat, organisme, del contingut població, del funcionament relacions continent/contingut i la científicament excellent Monografía estadística de la…
circumscriure
Matemàtiques
Traçar una figura que n’envolti una altra amb la qual tingui el major nombre de punts comuns possible.
Generalment hom circumscriu una corba superfície tancada a un polígon políedre que hi és contingut
espai connex
Matemàtiques
Espai topològic que no es pot expressar com a reunió disjunta de dos subespais oberts no buits.
Tot espai topològic arc-connex , és a dir, que donats dos punts de l’espai hi ha un arc de corba que els uneix contingut dins l’espai, és connex
atractor
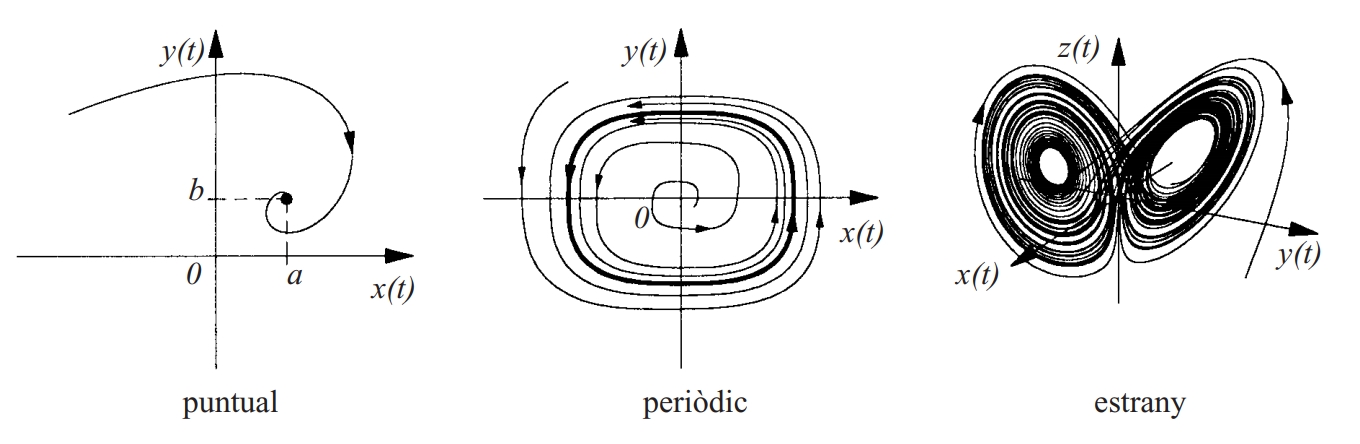
atractors
Matemàtiques
Estat o conjunt d’estats d’equilibri cap als quals convergeix un sistema dinàmic.
Formalment, donada una funció f , és un conjunt tancat E tal que f E és contingut en E , i per a alguns elements x d’un cert conjunt que conté E , la distància de f n E a E tendeix a zero quan n tendeix a infinit Normalment es requereix que l’òrbita de f sigui densa en E per a algun valor de x Si l’atractor E és un fractal es diu que és un conjunt estrany
Sergej Natanovič Bernstein
Matemàtiques
Matemàtic soviètic ucraïnès.
Estudià a París i a Göttingen Fou professor i director de l’Institut de Ciències Matemàtiques de Khàrkov 1917 i professor a la Universitat de Leningrad i membre de l’Acadèmia de Ciències de l’URSS A més dels seus treballs en teoria de funcions i equacions diferencials, fou un dels matemàtics, juntament amb Kolmogorov, que donà una axiomatització del càlcul de probabilitats, creant una construcció de tipus logicoformal independent del contingut semàntic de la probabilitat
teorema de la integral de Cauchy
Matemàtiques
Teorema relatiu a la integració en el camp complex que afirma que, per a tota funció f(z), de variable z complexa, holomorfa en un recinte simplement connex D, i per a qualsevol trajectòria tancada C continguda en D, es verifica: 72185.
Hom pot també enunciar aquest teorema dient que, en les condicions anteriors, la integral de f z entre dos punts de D és independent del camí d’integració elegit, sempre que aquest camí sigui contingut en D Aquest teorema és fonamental per a l’estudi de les funcions de variable complexa i dóna lloc a la teoria de la integració per residus integral Una aplicació immediata és la integral de Cauchy , mitjançant la qual hom pot expressar el valor d’una funció regular f z i de les seves derivades en un punt qualsevol a interior a un contorn al llarg de C , mitjançant les…
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l…
ascendent
Matemàtiques
Dit de la col·lecció indexada de conjunts en què cadascun és contingut en el següent rrespecte de la indexació.
subconjunt
Matemàtiques
Qualsevol conjunt contingut en un altre conjunt, és a dir, que tot element d’aquest ho és d’un altre.
Un subconjunt és una part d’un conjunt Si A és un subconjunt de B, hom ho representa així A⊆B La negació de A⊆B és representada per A⊄B El símbol ⊆és anomenat d’inclusió Tot conjunt admet els subconjunts trivials ell mateix i el conjunt buit ø La collecció de subconjunts d’un conjunt donat A forma un altre conjunt, dit conjunt de les parts de A , que hom representa per P A, i, per tant, PA = {BB⊆A} Si té n elements, PA en té 2 n