Resultats de la cerca
Es mostren 18 resultats
curvatura
Matemàtiques
En una corba plana, límit de la raó entre la variació de la inclinació de la tangent sobre un arc donat i la longitud d’aquest arc en fer-lo tendir a zero.
Analíticament, hom la defineix mitjançant l’expressió fx essent l’equació de la corba en coordenades cartesianes
radi de curvatura
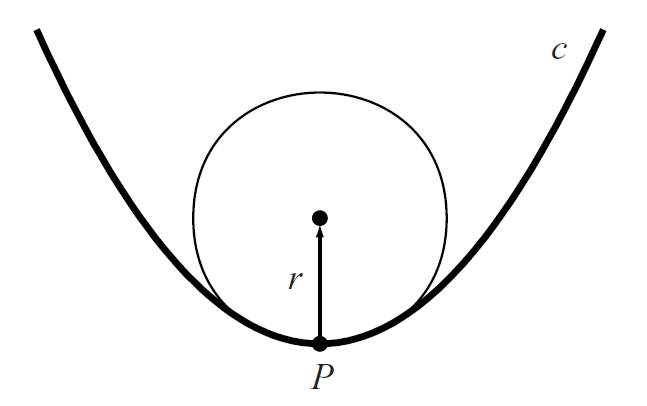
Radi de curvatura de la corba c en P
Matemàtiques
Invers de la curvatura d’una corba en un punt.
El radi de curvatura és el radi del cercle osculador
radi de curvatura
Matemàtiques
Radi d’una circumferència la curvatura de la qual coincideix amb la d’una corba en un punt donat.
Aquesta circumferència rep el nom de cercle de curvatura o bé cercle osculador El valor R del radi de curvatura és l’invers de la curvatura C El centre del cercle osculador rep el nom de centre de curvatura de la corba
cercle osculador
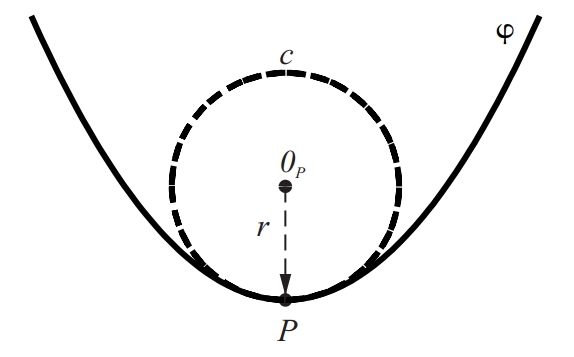
Cercle osculador de la corba φ en el punt P
Matemàtiques
En un punt d’una corba, cercle del pla osculador que té les mateixes tangent i curvatura que la corba en aquest punt.
tensor de Riemann
Física
Matemàtiques
Tensor una vegada contravariant i tres vegades covariant.
Definit per on { ijk } són els símbols de Christoffel de segona classe, lligats a l’espai de Riemann, on és considerada una forma diferenciable
evoluta
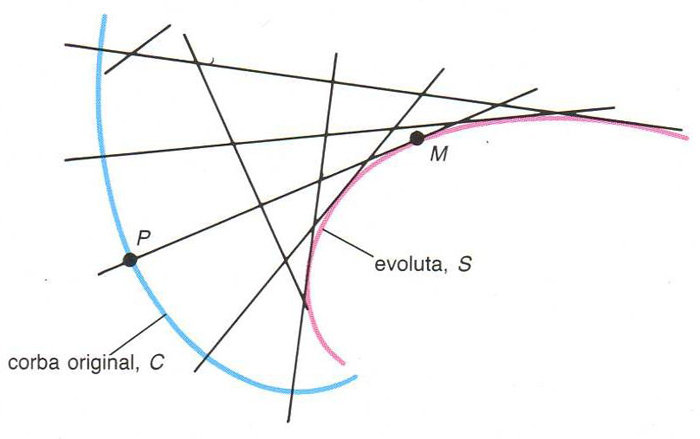
La corba S és l’evoluta de C
© fototeca.cat
Matemàtiques
Donada una corba plana C
, lloc geomètric dels centres de curvatura de C
.
És l'envolupant S de les normals a la corba C així, una normal en el punt P a C és tangent a l’evoluta i el punt de tangència M és el centre de curvatura de C en el punt P Si S és l’evoluta de C , C és una evolvent de S L’evoluta d’un cercle es redueix a un punt
oval
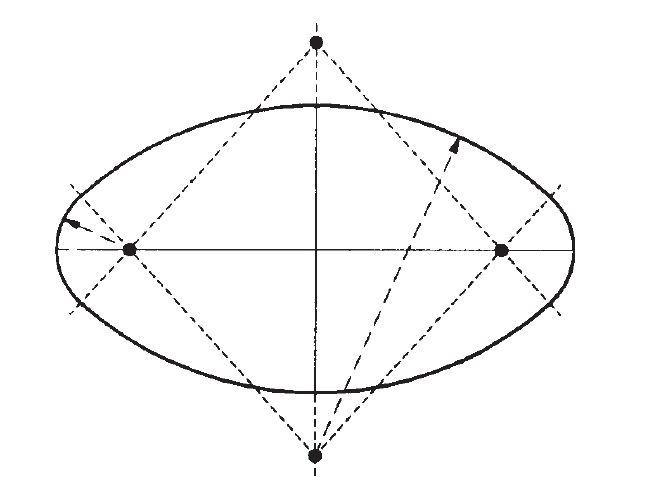
oval
Matemàtiques
Corba amb segona derivada contínua, plana i tancada, en la qual el vector de curvatura és dirigit, en tots els punts, cap a l’interior i, per tant, és completament convexa.
Els punts en què la curvatura passa per màxims i mínims relatius són anomenats vèrtexs de l’oval, i hom demostra que tot oval en té quatre o més Exemples d’oval són les ellipses i el perfil dels ous de gallina
punt umbilical
Matemàtiques
Punt d’una superfície per al qual la recta normal a ella és aresta d’un feix de plans, els quals tallen la dita superfície segons corbes que tenen, en aquest punt, el mateix radi de curvatura.
En la superfície esfèrica, tots els punts són umbilicals Si tots els radis de curvatura tenen el mateix sentit, el punt és anomenat ellíptic , mentre que si hi ha curvatures de sentits diferents el punt és hiperbòlic En els punts umbilicals, cada recta tangent a la superfície és perpendicular a la seva conjugada
tríedre de Frenet
Matemàtiques
Tríedre trirectangle constituït pels vectors tangent, normal i binormal a una corba en un punt.
Donada una corba C , parametritzada per l’abscissa curvilínia s s dona la longitud de l’arc des d’un punt de referència de la corba, C s = x s , y s , z s , tríede ortonormal directe definit en cada punt P de C pels vectors tangent t , normal n i binormal b , l’expressió dels quals és t = d C s / ds P , ∥ t ∥=1 n = d t / ds /∥ d t / ds ∥ P , ∥ n ∥=1 b = t ∧ n , ∥ b ∥=1 El pla P , t , n és el pla osculador de la corba C en el punt P , el pla P , n , b és el pla normal de C en P , i el pla P , b , t és el pla rectificador de C en P El radi de curvatura de C és R s =…
Jean Meusnier de la Place
Física
Matemàtiques
Físic i matemàtic francès.
Collaborà amb Lavoisier en els cèlebres experiments que donaren lloc a la descomposició de l’aigua en oxigen i hidrogen i a la seva ulterior síntesi Continuà les investigacions matemàtiques de Monge en un estudi que féu sobre la curvatura de les superfícies hi ha el teorema que porta el seu nom