Resultats de la cerca
Es mostren 9 resultats
adherència
Matemàtiques
Conjunt associat a un subconjuntd’un espai topològic format per tots els punts adherents al suconjunt.
Si A denota el conjunt, l’adherència es denota per Ā És el mínim conjunt tancat que conté A Així Ā = A si, i solament si, A és tancat
esfera
Matemàtiques
En un espai mètric de distància d, conjunt de punts x la distància dels quals a un cert punt fix p és igual a un nombre real positiu r.
El centre de l’esfera és p i el radi r , i es denota per S p r A ℝ n l’esfera de centre 0 i radi 1 es denota per S n –1 i rep el nom d’ esfera unitat
ortogonal
Matemàtiques
En un espai vectorial, dit dels subconjunts A i B quan cada vector de A és ortogonal a tots els vectors de B
.
Si A és ortogonal a B , hom ho denota per A ⊥ B
àlgebra
Matemàtiques
Anell B que esdevé un A-mòdul a causa d’un homomorfisme entre un anell A i B.
Tot anell és sempre una ℤ-àlgebra, en què ℤ denota l’anell dels nombres enters
digraf
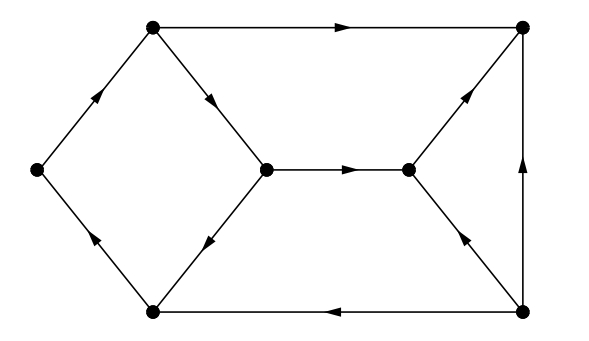
digraf
Matemàtiques
Graf les arestes del qual, anomenades arcs, són parells ordenats de vèrtexs diferents.
Un digraf G amb un conjunt de vèrtexs V i un conjunt d’arcs E es denota per G = V , E Sovint s’escriu també E = E G i V = V G
bola
Matemàtiques
En un espai mètric amb una distància d, conjunt de punts x la distància dels quals a un cert punt fix a és menor (o igual) que un nombre fix r (r > 0); es parla, aleshores, de la bola oberta (tancada) de radi r i de centre a.
Usualment es denota per B a r la bola oberta i per B̄ a r la bola tancada A ℝ les boles obertes són els intervals oberts i les boles tancades són els intervals tancats
inclusió
Matemàtiques
Relació d’ordre parcial entre conjunts, notada mitjançant el símbol ⊂(o, a vegades, ⊆), definida per la condició A⊂B (o A⊆B) si i només si tots els elements de A pertanyen a B
.
En aquest cas, hom diu que el conjunt A és inclòs en el conjunt B o que A és un subconjunt de B Si A no és inclòs en B , hom ho denota per A ⊄ B
trencat
Matemàtiques
Nombre que denota un agregat de parts alíquotes d’una unitat, per mitjà de dos enters a i b, que hom escriu a/b
.
El nombre a és el numerador , i b , el denominador És conegut també com a nombre fraccionari fracció, nombre racional
espai vectorial
Matemàtiques
Grup abelià E
en el qual hi ha definida una llei de composició externa amb elements d’un cos K
, K
× E
→ E tal, que al parell (λ, e
) correspon l’element λ e
.
I acomplint-se les propietats λ + μ e = λ e + μ e , λ e + f = λ e + λ f , λμ e = λμ e i 1 e = e Els elements de E són anomenats vectors , i els elements de K , escalars Una part de E que sigui subgrup respecte a la suma i que sigui estable respecte al producte per qualsevol escalar, és anomenada subespai de E , i amb les mateixes operacions de E és un altre espai vectorial Si F és un subespai de E , hom pot definir congruències a E mitjançant la relació d’equivalència x ≡ y mòd F , si i només si la diferència x — y pertany a F Això permet de formar el conjunt quocient E/F quocient, el…